Fecha de la ultima revisión

## [1] "2023-07-10"

Activar las librerias, averiguar que TIENE instalado estos paquetes

library(QuantPsyc)
library(car)
library(boot)
library(ggplot2)
library(tidyverse)
library(sjPlot)

Regresión Lineal

La regresión lineal es el modelo básico de evaluar si hay una relación lineal o sea recta entre dos variable. Esta relación entre las variables puedes ser positiva o negativa. Hay otro tipos de regresión, que incluye regresión no lineal tal como cuadrática \[x^2\] o cúbica \[x^3\], logarítmica \[log(x)\] entre muchas otras alternativas.

Aquí estaremos evaluando solamente la regresión lineal

Primero paso es subir los datos:

El números de barres en un bario y la cantidad de asesinados en este barrio (Datos ficticios)

library(readr)
pubs <- read_csv("Data_files_csv/pubs.csv")
pubs

pubs	mortality
10	1e+03
20	2e+03
30	3e+03
40	4e+03
50	5e+03
60	6e+03
70	7e+03
500	1e+04

# Cambiamos los nombres de las columnas

pubs=pubs%>%
  dplyr::rename(barres=pubs, mortalidad=mortality)

la función lm()

Como hacer un regresión lineal (Linear Regression) simple, usando la función lm(), para “linear model”= modelo lineal. Una regresión necesita dos variable continuas (vea el módulo de correlación). Es importante que estas variable tenga una distribución normales. La diferencia entre una correlación y una regresión es que la primera es un análisis que describe el patrón y en la segunda es que no solamente describe el patrón pero hace predicción sobre la relación entre las variables. Usando la regresión uno calcula tambien una linea que describe la relación entre las variables. Esta variable se puede describe como $y=m_x+b$ donde la m representa la pendiente y la b representa el intercepto. También lo pueden ver en libros de la siguiente forma $y=\alpha+\beta_x$ donde la $\beta$ beta representa la pendiente y la $\alpha$ el intercepto.

La formula de lm() se compone de lm(y~x, data= “df”). Nota la tilde ~. Hay dos pruebas la priemra para determinar si $\alpha$ es distinto de cero. La hipótesis nula es

Ho: el intercepto $\alpha$ es igual a cero Ha: el intercepto, $\alpha$ no es igual a cero. Entonces el punto donde la linea intercepta el cero puede estar mayor de o menor de cero.

La segunda hipótesis nula es que la pendiente es diferente de cero, esto quiere decir que la pendiente no sugiere un patrón de aumentar y disminuir entre las dos variables.

Ho: la pendiente $\beta$ es igual a cero Ha: la pendiente, $\alpha$ no es igual a cero. Entonces la relación entre las dos variables es o positiva o negativa.

Ahora evaluamos los resultados de la regresión entre el número de barres en un vecindarios y la mortalidad en este mismo sector. Se observa que los coeficientes de la linea son $y=3352+14.3*x$. Entonce el intercepto en cero comienza en 3352 fatalidades y por cada bar suplementario hay 14.3 más fatalidad.

Ahora para determinar si estos valores son significativo hay que evaluar el valor de p en cada linea. La hipótesis nula del intercepto tiene un valor de p =0.005, que sugiere que se debería rechazar la hipótesis nula, y por consecuencia aceptamos la hipótesis alterna. La pendiente tiene un valor de p=0.015 y también se rechaza la hipotesis nula.

pubReg <- lm(mortalidad~barres, data = pubs) 

#summary(pubReg) # Si no se acuerda de la funcíon que sigue

tab_model(
  pubReg,show.df = TRUE,
  CSS = list(
    css.depvarhead = 'color: red;',
    css.centeralign = 'text-align: left;', 
    css.firsttablecol = 'font-weight: bold;', 
    css.summary = 'color: blue;'
  )
)

	mortalidad
Predictors	Estimates	CI	p	df
(Intercept)	3351.96	1440.34 – 5263.57	0.005	6.00
barres	14.34	3.82 – 24.86	0.016	6.00
Observations	8
R² / R² adjusted	0.649 / 0.591

Visualización de la regresión

Se observa que hay un aumento en fatalidades con aumento en el número de barres. Pero nota el valor a la derecha que parece ser muy atípico comparado a los otros.

ggplot(pubs, aes(x=barres, y=mortalidad))+
  geom_smooth(method = lm)+ # modelo lineal
  geom_point()

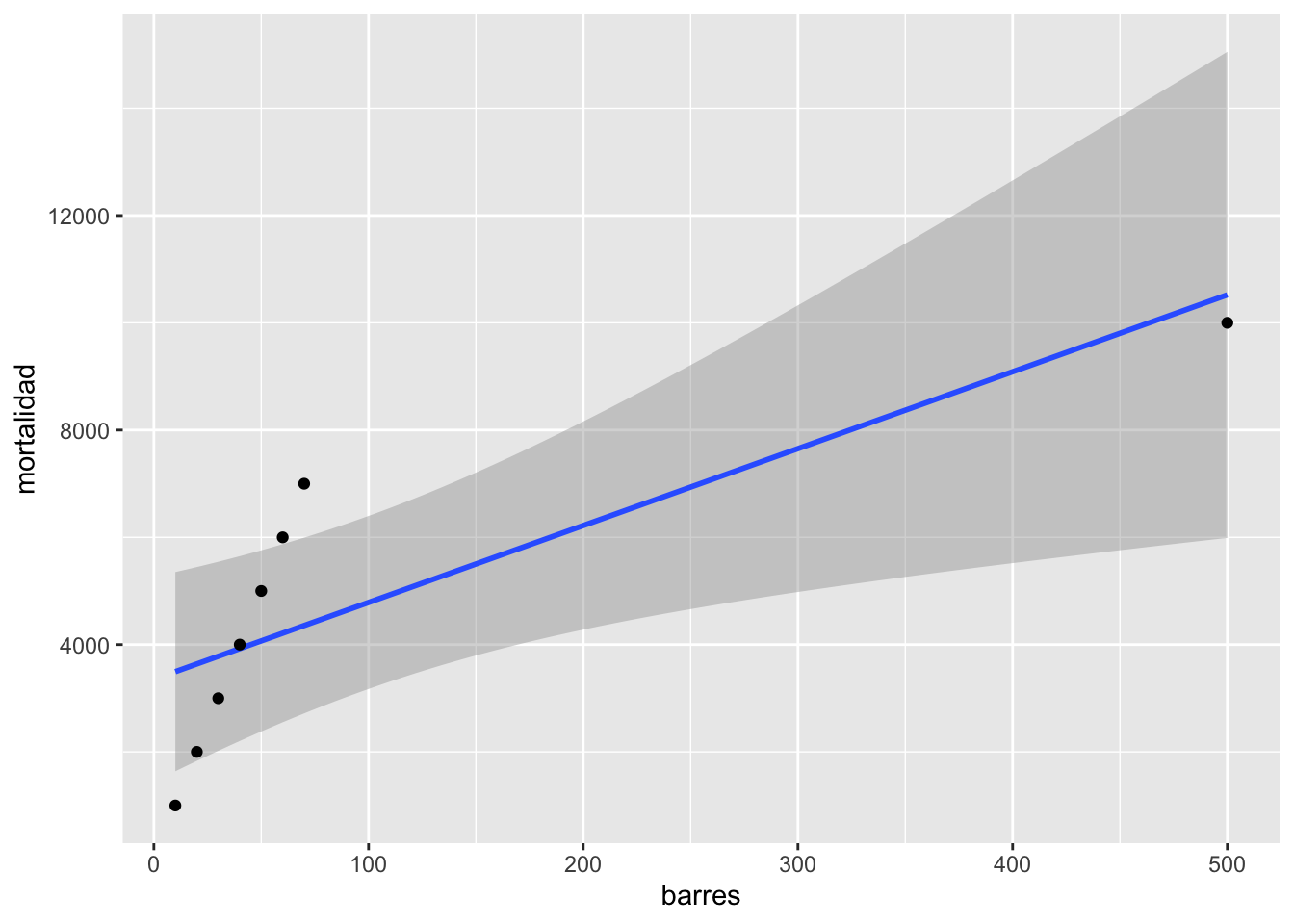
El impacto de valores atípico

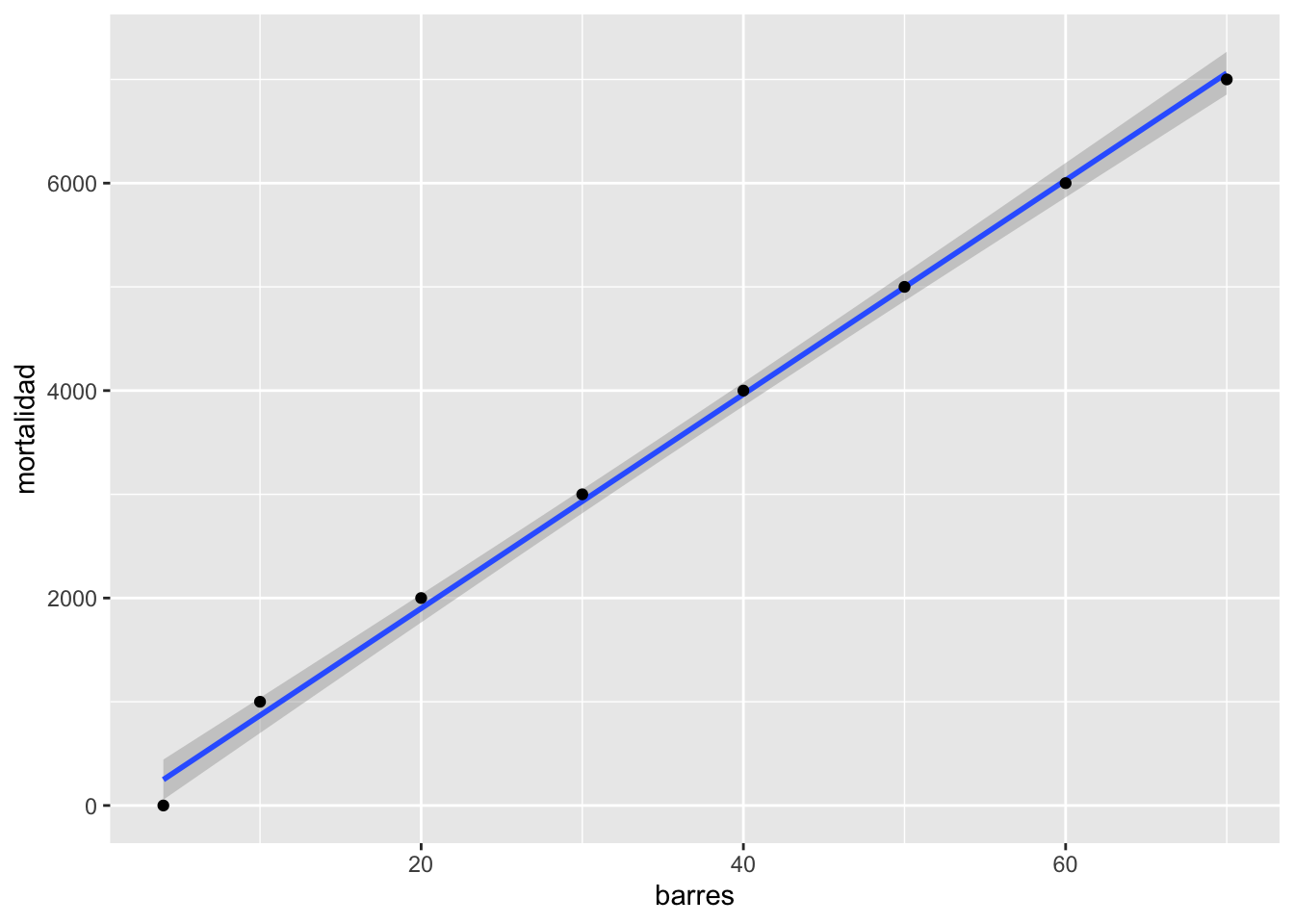
En cierta ocasiones valores fuera de lo normal pueden hacer grandes cambios en el resultado, en este caso la regresión. ¿Cual es el efecto del valor grande? Removemos ese valor del archivo de datos y revaluamos el modelo (la regresión lineal). Nota que ahora el modelo es sumamente diferente $y=-163.7+103.2*x$. ¿Ahora se rechaza las dos hipótesis?

pubsnew <- pubs[ which(pubs$barres<80), ]  # remover el valor grande

pubsnew=pubsnew %>% 
  add_row(barres = 4, mortalidad = 0) # Añadiendo un par de valores


pubRegNew <- lm(mortalidad~barres, data = pubsnew)
#summary(pubRegNew)

tab_model(
  pubRegNew,show.df = TRUE,
  CSS = list(
    css.depvarhead = 'color: red;',
    css.centeralign = 'text-align: left;', 
    css.firsttablecol = 'font-weight: bold;', 
    css.summary = 'color: blue;'
  )
)

	mortalidad
Predictors	Estimates	CI	p	df
(Intercept)	-163.70	-374.14 – 46.73	0.106	6.00
barres	103.20	98.18 – 108.23	<0.001	6.00
Observations	8
R² / R² adjusted	0.998 / 0.997

ggplot(pubsnew,aes(x=barres, y=mortalidad))+
  geom_smooth(method=lm)+
  geom_point()

La venta de discos de música

Ahora un set de datos más complejo y más realista a los que uno encontraría en un estudio de en medicina, sociología o ecológica.

Los datos representa la cantidad de dinero dedicado a la promoción de diferentes CD’s de una compañia de música y la cantidad de CD (CD/downloads) vendido. El la primera linea se observa la cantidad de libras esterlina, £ (UK) dedicado a la promoción del album de música, en la primera linea vemos que se gasto £10,256, y después la cantidad de CD vendido fue 330.

library(readr)
Album_Sales_1_new <- read_csv("Data_files_csv/Album_Sales_1_new.csv")
head(Album_Sales_1_new)

adverts	sales
10.3	330
986	120
1.45e+03	360
1.19e+03	270
575	220
569	170

length(Album_Sales_1_new$adverts)  # cuantas files de datos hay en el data frame

## [1] 200

Comenzamos con hacer un gráfico entre las dos variables. Nota que en la parte de geom_smooth(), tiene que incluir method=lm, esto significa que el método de construir la linea usara la regresión lineal. Se añade a la función lineal $\epsilon$ que representa los errores de los valores al comparar con la linea que representa el mejor modelo.

\[Y_{ i }=\beta _{ 0 }+\beta _{ 1 }X_{ i }+\epsilon _{ i }\] Recuerda que $\beta _{ 0 }$ es el intercepto y el $\beta _{ 1 }X_{ i }$ es la pendiente. El área sombreada es el área de 95 de intervalo de confianza. Esto quiere decir que la mejor linea, intercepto y pendiente podría variar en este rango si repetimos el experimento. Nota aquí todas las alternativas, añadí los dos extremos, con una pendiente mayor (roja) y una menor (violeta). Cada punto representa la venta de CD con su correspondiente cantidad dedicada a la promoción. Los $epsilon$ seria la diferencia entre la mejor linea y el valor original, esto se llama tambien los residuales.

library(ggplot2)
ggplot(Album_Sales_1_new,aes(x=adverts, y=sales))+
  geom_smooth(method=lm, se = TRUE)+
  geom_point()+
  geom_segment(aes(x=0, y=120, xend=2250, yend=380), colour="red")+
  geom_segment(aes(x=0, y=150, xend=2250, yend=320), colour="purple")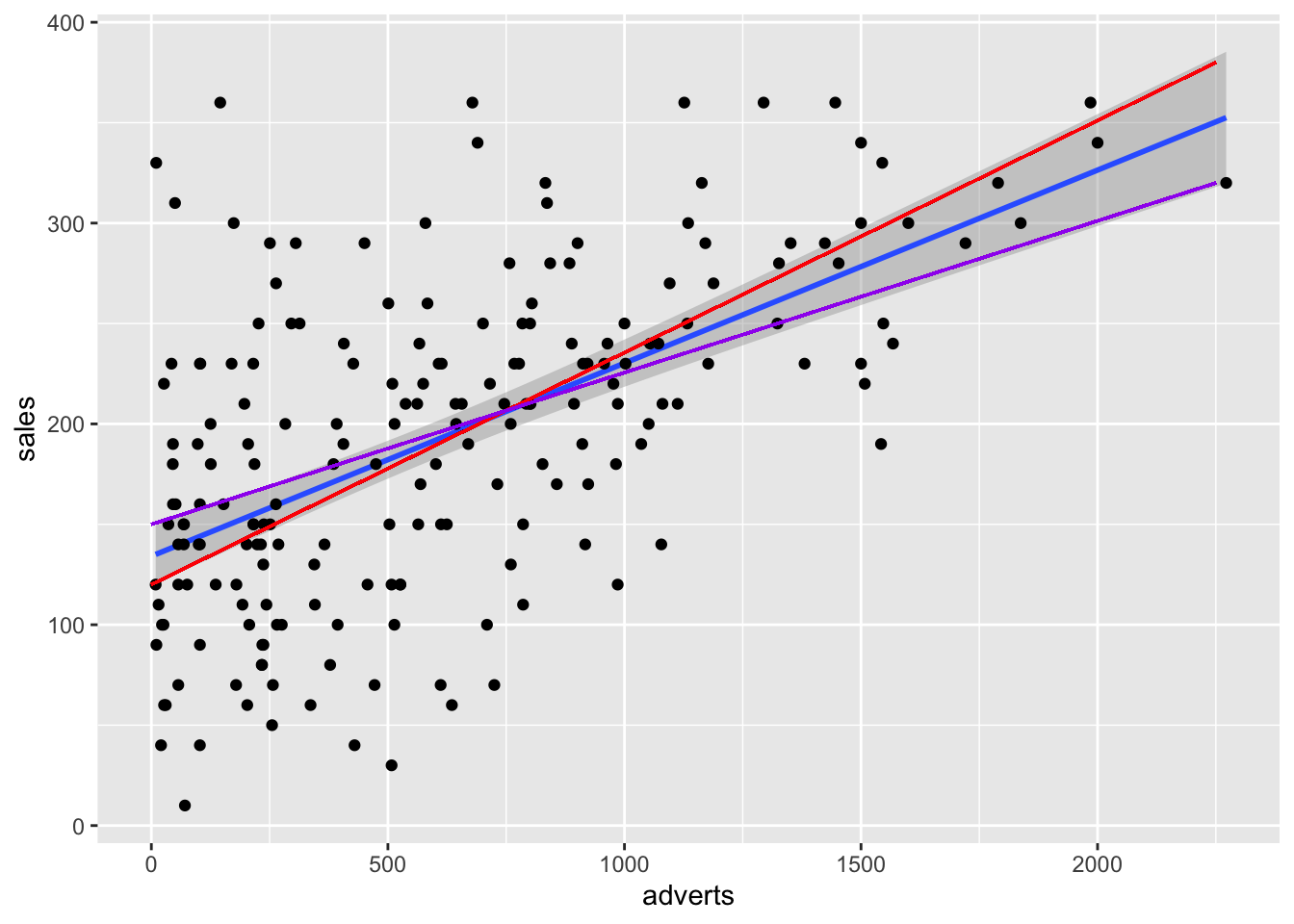

El modelo lineal con la función lm(). ¿Como interpretas los coeficientes y si estos son significativos, si se rechaza la hipótesis nula?

library(sjPlot)
head(Album_Sales_1_new)

adverts	sales
10.3	330
986	120
1.45e+03	360
1.19e+03	270
575	220
569	170

model1=lm(sales~adverts, Album_Sales_1_new)

#summary(model1)

tab_model(
  model1,show.df = TRUE,
  CSS = list(
    css.depvarhead = 'color: red;',
    css.centeralign = 'text-align: left;', 
    css.firsttablecol = 'font-weight: bold;', 
    css.summary = 'color: blue;'
  )
)

	sales
Predictors	Estimates	CI	p	df
(Intercept)	134.14	119.28 – 149.00	<0.001	198.00
adverts	0.10	0.08 – 0.12	<0.001	198.00
Observations	200
R² / R² adjusted	0.335 / 0.331

Supuestos de la regresión lineal

Igualdad de varianza: En el primer gráfico evaluar si los datos están distribuido más o menos igual. y que no un más variación un un área del gráfico que otro.
Normalidad de los datos: En el segundo gráfico evaluar la figura de qqplot.
Evaluar si hay datos sesgados (atípicos) que influencia los resultados
En el cuarto gráfico evaluar si hay valores que tienen mucho peso si se incluyen o no en el análisis. Estos van a ser identificado

En el presente gráfico hay tres valores que hay que evaluar (1,42,169), estos valores se tiene que asegurar que son correctos. Siempre es bueno remover los valores sesgados y rehacer el análisis para observar cuan diferente son los resultas.

plot(model1)  # Evaluar los supuestos, 1. Igualdad de varianza, 2. Normalidad, 4. Datos sesgados (Cook's Distance)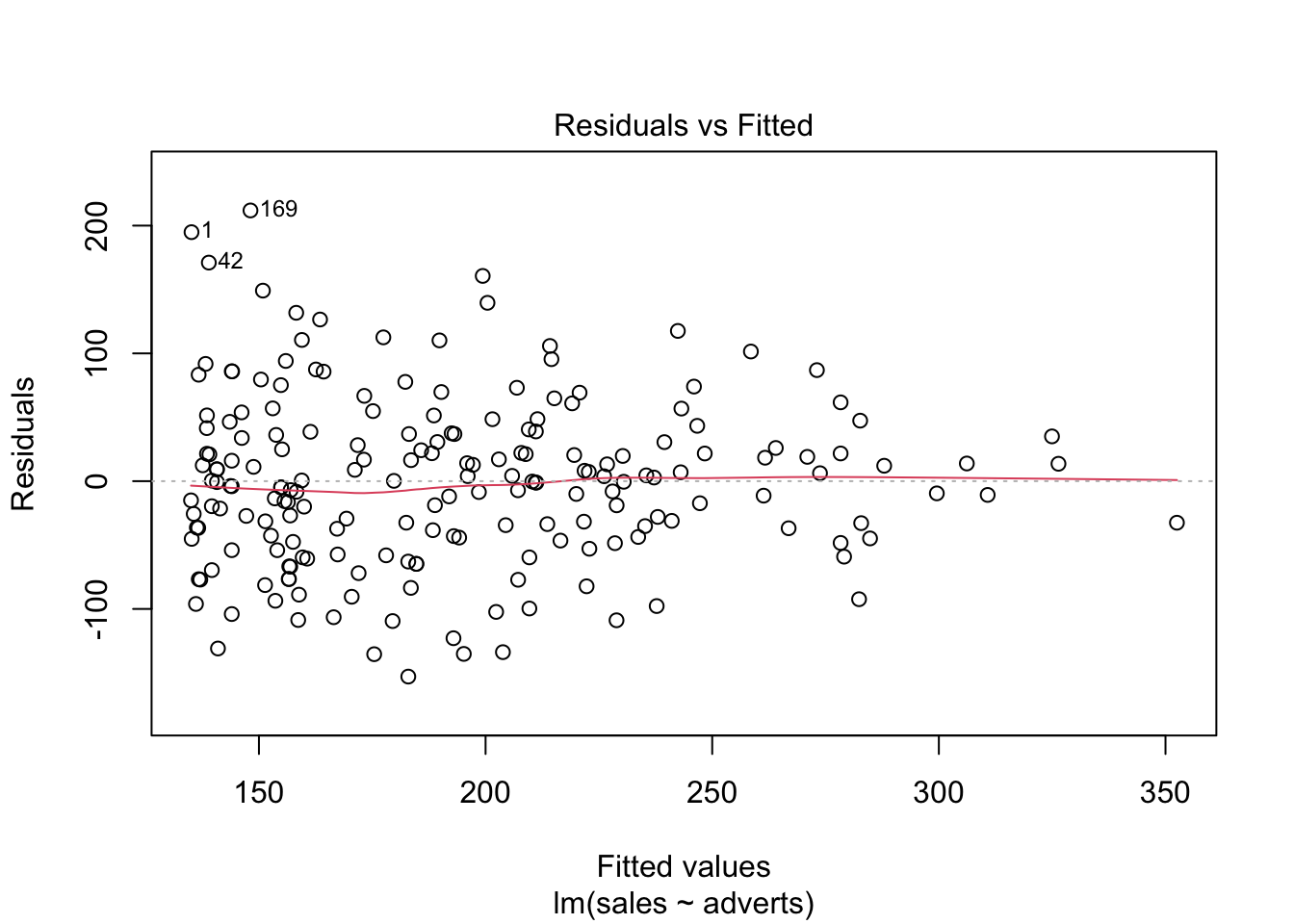

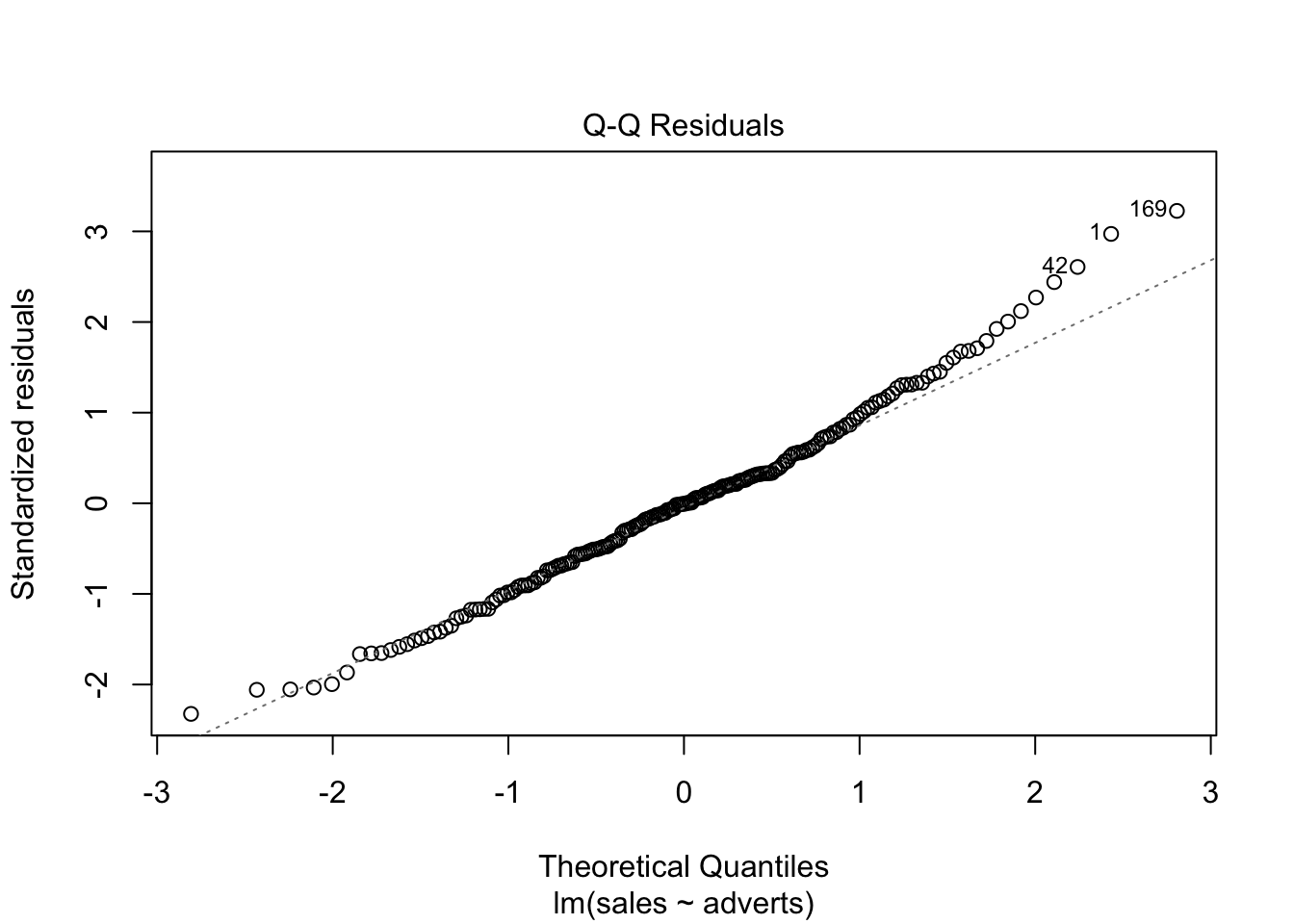
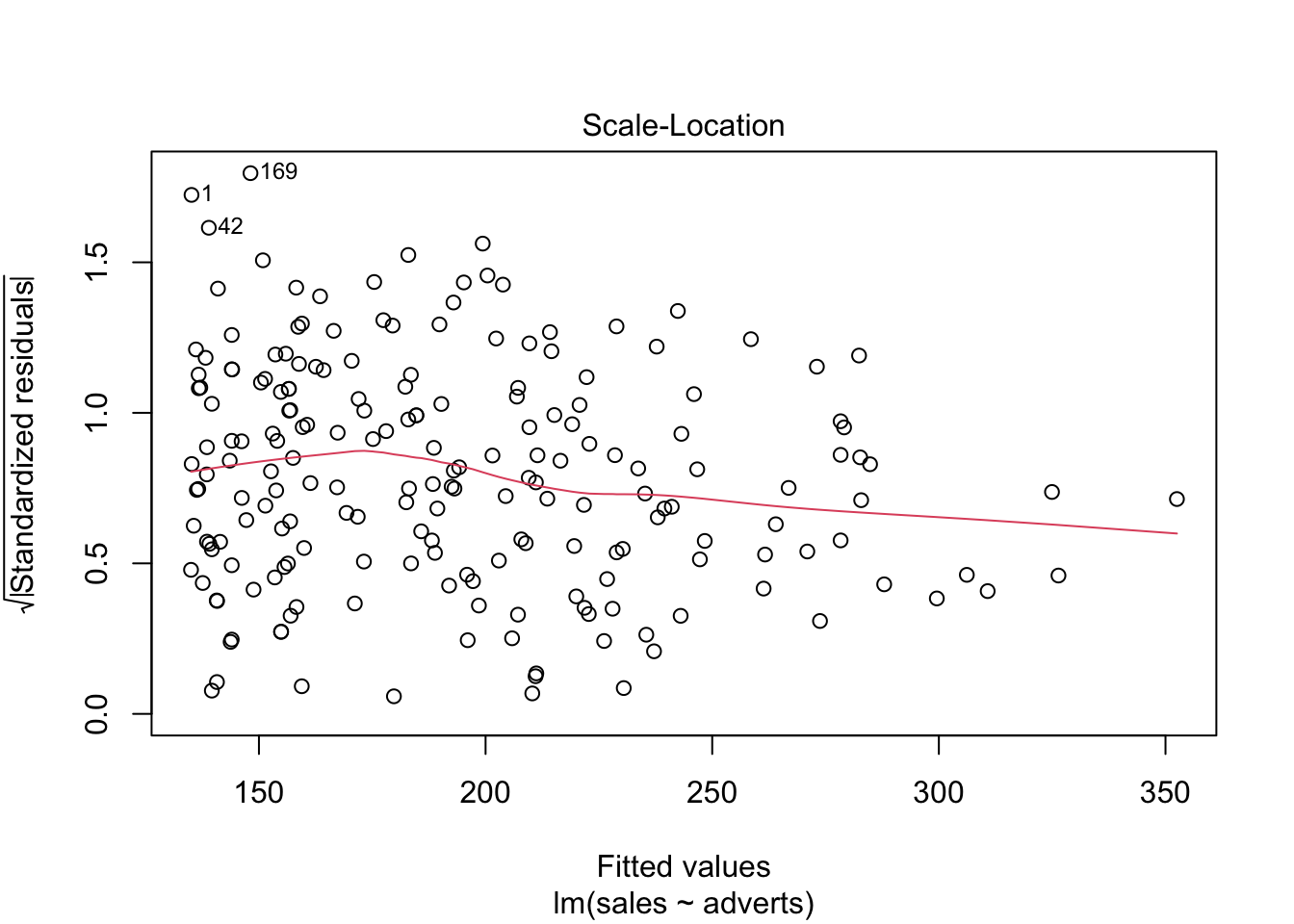
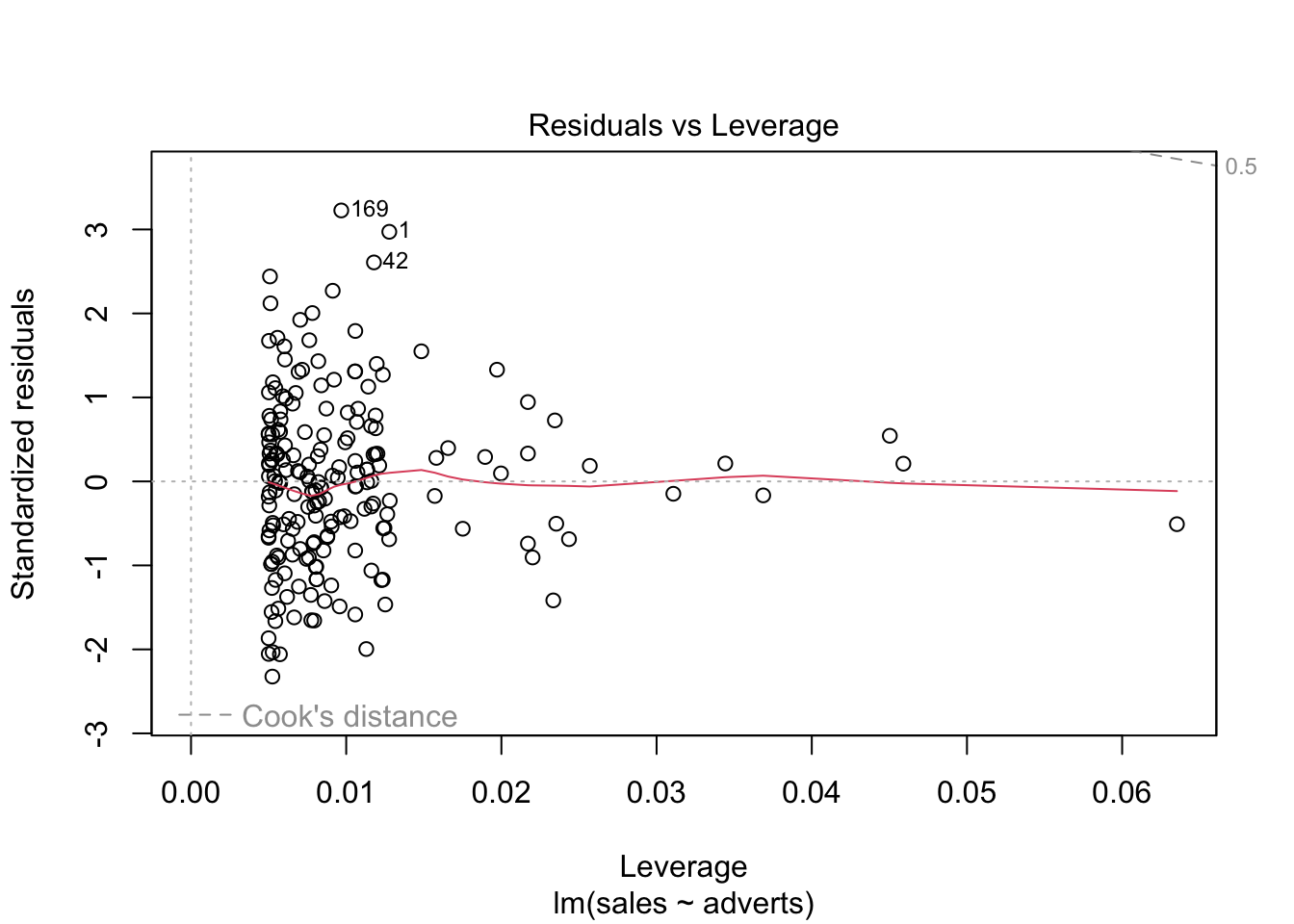
Cook’s Distance

Evaluar si hay unos valores que sesgan los resultados.

FROM WIKIPEDIA Definition. Data points with large residuals (outliers) and/or high leverage may distort the outcome and accuracy of a regression. Cook’s distance measures the effect of deleting a given observation. Points with a large Cook’s distance are considered to merit closer examination in the analysis.

Detecting highly influential observations There are different opinions regarding what cut-off values to use for spotting highly influential points. A simple operational guideline of D_i>1 has been suggested.

Others have indicated that D_i>4/n, where n is the number of observations, might be used.

Aqui enseño como añadir 1. los valores de “cook.distance” a su archivo 2. Añadir una columna de “secuencia” de los datos 3. Crear una gráfica de las distancia de Cook.
4. Which values have Di larger than 1, which values have Cook’s distances larger 4/n?

4/length(Album_Sales_1_new$adverts)

## [1] 0.02

Album_Sales_1_new$cooks.distance<-cooks.distance(model1)
head(Album_Sales_1_new)

adverts	sales	cooks.distance
10.3	330	0.0572
986	120	0.011
1.45e+03	360	0.0178
1.19e+03	270	0.000662
575	220	0.000548
569	170	0.000207

Album_Sales_1_new$sequence=c(1:200)
head(Album_Sales_1_new)

adverts	sales	cooks.distance	sequence
10.3	330	0.0572	1
986	120	0.011	2
1.45e+03	360	0.0178	3
1.19e+03	270	0.000662	4
575	220	0.000548	5
569	170	0.000207	6

tail(Album_Sales_1_new)

adverts	sales	cooks.distance	sequence
701	250	0.00141	195
911	190	0.000804	196
889	240	0.000321	197
801	250	0.00101	198
1.5e+03	230	0.00608	199
786	110	0.00649	200

ggplot(Album_Sales_1_new, aes(sequence, cooks.distance))+
  geom_point()+
  geom_hline(aes(yintercept=4/length(Album_Sales_1_new$adverts), colour="red"))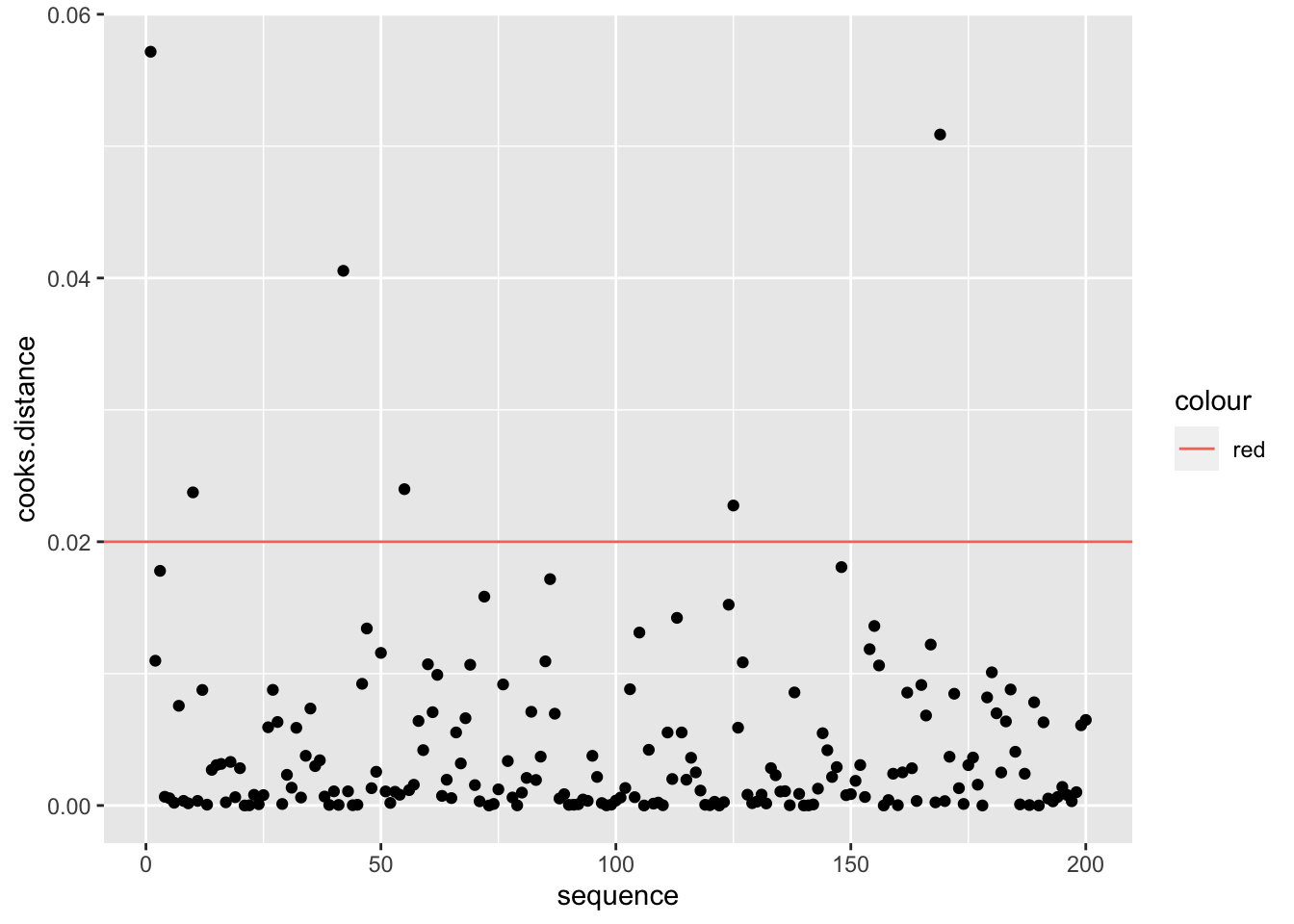

Repaso de los PASOS

Paso 1

Primer paso, mirar los coeficientes.

El resultado: El coeficiente (intercepto) y la pendiente del model1

Paso 2

Evaluar si los coeficientes son diferentes de cero.

La primera hipótesis, Determinar si el intercepto es igual a cero. Mira el valor de p, Pr(>|t|), determinar si el valor es menor de 0.05, si lo es se rechaza la Ho y por consecuencia tenemos confianza que el intercepto no incluye cero.
La segunda hipótesis nula Deteminar si la pendiente es igual a cero. Mira el valor de p, Pr(>|t|), como el valor es menor de p=0.05, se rechaza la Ho y por consecuencia tenemos confianza que la pendiente no incluye cero.

Paso 3

Evaluar si los datos cumple con los supuestos.
Igualdad de varianza, usa la gráfica de residuales
Normalidad, qqplot
Valores sesgados, la prueba de Cook’s

advertizingReg <- lm(sales~adverts, data = Album_Sales_1_new)
summary(advertizingReg)

## 
## Call:
## lm(formula = sales ~ adverts, data = Album_Sales_1_new)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -152.949  -43.796   -0.393   37.040  211.866 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 1.341e+02  7.537e+00  17.799   <2e-16 ***
## adverts     9.612e-02  9.632e-03   9.979   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 65.99 on 198 degrees of freedom
## Multiple R-squared:  0.3346, Adjusted R-squared:  0.3313 
## F-statistic: 99.59 on 1 and 198 DF,  p-value: < 2.2e-16

tab_model(
  advertizingReg,show.df = TRUE,
  CSS = list(
    css.depvarhead = 'color: red;',
    css.centeralign = 'text-align: left;', 
    css.firsttablecol = 'font-weight: bold;', 
    css.summary = 'color: blue;'
  )
)

	sales
Predictors	Estimates	CI	p	df
(Intercept)	134.14	119.28 – 149.00	<0.001	198.00
adverts	0.10	0.08 – 0.12	<0.001	198.00
Observations	200
R² / R² adjusted	0.335 / 0.331

Alternativa para Gráficar los residuales

Plot the residuals and the fitted values

Evaluating residuals:

If we observe that the residuals are randomly distributed (no pattern, a straigth line), then we can assume that there is equality of variance along the “x” axis.

Definition of Residuals

A quantity remaining after other things have been subtracted or allowed for. FROM Wikipedia

A residual (or fitting deviation), on the other hand, is an observable estimate of the unobservable statistical error.

# "advertizingReg", nota que este no es un data frame pero un modelo
# The main figure
ggplot(Album_Sales_1_new,aes(x=adverts, y=sales))+
  geom_smooth(method=lm, se = TRUE)+
  geom_point()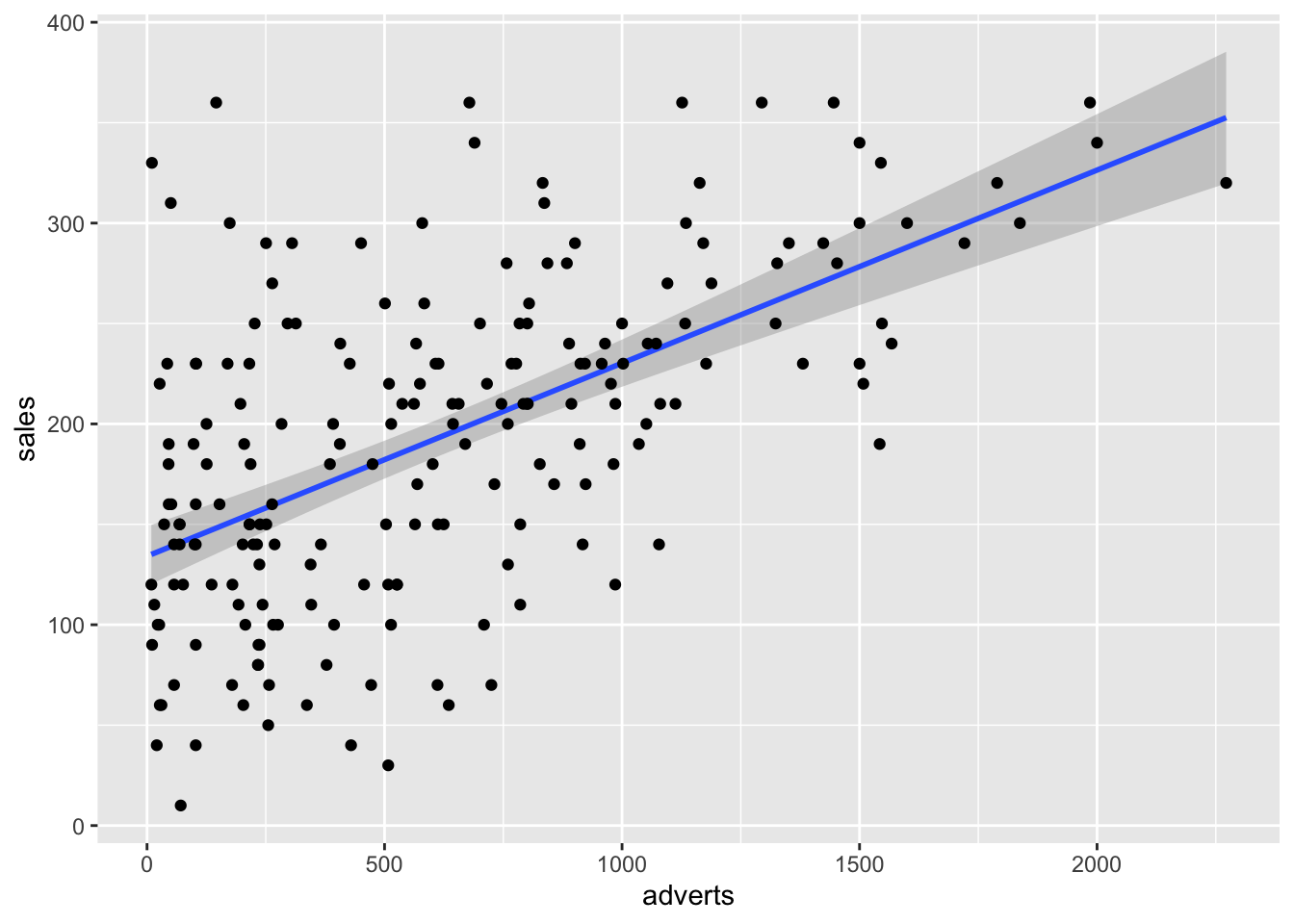

# Graficando los residuales, metodo 1
ggplot(model1, aes(x=.fitted, y=.resid))+
  geom_point()+
  geom_smooth(method=lm)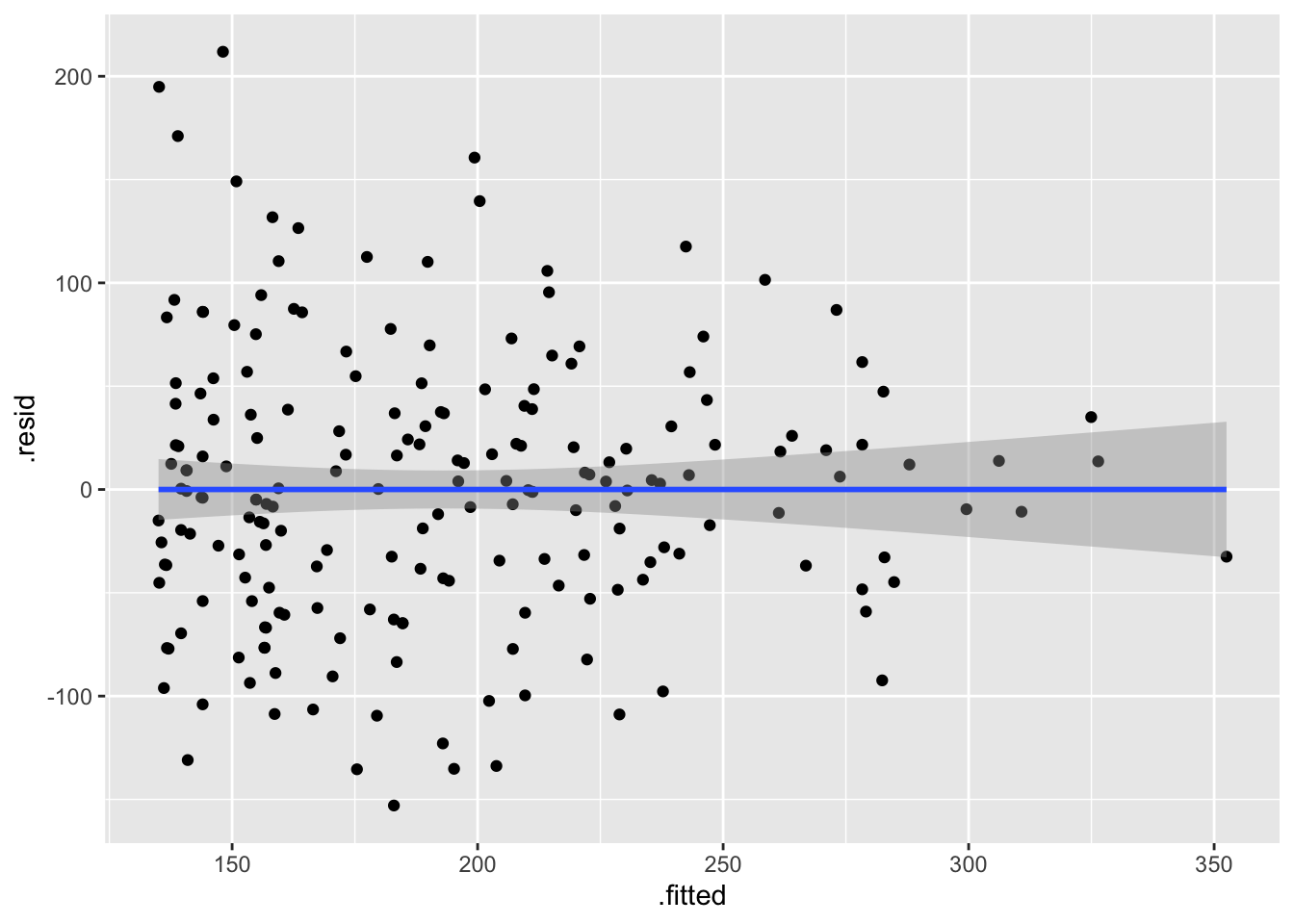

Porque podemos usar la alternativas anterior

Cuando R corre un analisis, hace muchos calculos y guarda parate de estos calculos como lista de datos.

Para ver algunos de los valores calculado uno pone el nombre del modelo y la añade el $ y deberia aparecer la lista de los valores calculados. o otra alternativa es usar la función ls() = list() para ver el nombre de las variables

ls(model1)

##  [1] "assign"        "call"          "coefficients"  "df.residual"  
##  [5] "effects"       "fitted.values" "model"         "qr"           
##  [9] "rank"          "residuals"     "terms"         "xlevels"

# model1$residuals  # Por ejemplo para ver los residuales del modelo

Ejercicio #1

Usa los enviado por MSTeam llamado “Alturas_Humanos

En este archivo vemos tres columnas. Genero, Altura de la persona (Altura_cm) y Peso de la persona (Peso_kg)
Evalua cada paso para determinar si hay una relación entre la altura y el peso de las personas.
Haz un gráfico de la relación entre la altura y el peso
Evalúa el modelo de regresión entre las dos variables
Evalúa los supuestos

library(readr)
Alturas_Humanos <- read_csv("Data_files_csv/Alturas_Humanos.csv")

head(Alturas_Humanos)

Genero	Altura_cm	Peso_kg
Hombres	174	96
Hombres	189	87
Mujer	185	110
Mujer	195	104
Hombres	149	61
Hombres	189	104

Ejercicio #2

Datos sobre la orquidea Dipodium

Los datos se encuentra en el paquete ggversa debajo el nombre de dipodium.

Evalua todos los pasos para ver si la altura de inflorescencia es un predictor de la cantidad de flores que tiene una planta.

T14_Regression