Fecha de la ultima revisión

## [1] "2023-07-10"

Activar los Paquetes

library(ggplot2)  # paquete para visualizar los datos
library(ggversa) # paquete para diferentes conjuntos de datos
library(modeest) # paquete para calcular la moda 

library(pastecs) # paquete para análisis tiempo-espacial usado en ecología 
library(psych) # paquete para análisis psicométrica, psicológica y de personalidad 
library(knitr) # un grupo de función para incluyendo tablas bonitas con kable.
library(tidyverse)
library(gridExtra)
library(e1071)

Estadistica descriptiva

En los módulos de “Medidas de Tendencias Central” y “Medidas de Dispersión” se explicó donde proviene estos parámetros y como calcular estos. En este módulo aprenderemos diferentes funciones como calcular estos parámetros individualmente y herramienta como calcular todos y otros parámetros todo juntos.

Los indices que veremos aquí incluye

el promedio
la mediana
la desviación estándar
el mínimo
el máximo
los cuantiles
el indice Oblicuidad (en ingles “Skewness”)
el indice de Curtosis ( en ingles “Kurtosis”)

Aqui creamos un conjunto de datos de 100 datos con un promedio de 100 y una desviación estándar de 10. Nota que la función set.seed() es que el comienzo la simulación sea igual a cada vez que se corre, y se el mismo resultado. Esto se añade solamente cuando uno esta enseñando y que los resultados sean consistente.

x=rnorm(100, 100, 10) #(100 datos, x=100, sd=10)
x=data.frame(x)
head(x)

x
110
96.1
102
112
119
105

mean(x$x) # el promedio

## [1] 100.0398

sd(x$x) # la desviación estándar

## [1] 9.932391

min(x$x) # el valor mínimo

## [1] 77.74019

max(x$x) # el valor máximo

## [1] 123.6114

Quiz 1: Usa R y construye una lista o data frame con los siguientes datos y calcular el promedio. Contesta en MSTeam Form con tu respuesta. 4, 6, 7, 3, 9, 10, 19, 52.

Analisis con muchos datos

Usaremos datos que hemos visto en el modulo Producción de Gráficos.

Se necesita el archivo DownloadFestival que se encuentra debajo la pestaña de Los Datos. El ejemplo proviene de Field et al. (2014).

Una bióloga estaba preocupado por los posibles efectos sobre la salud de los que particpan a un festivales de música. Entonces, un año fue al Download Festival en el Reino Unido (Download Festival UK). Ella midió la higiene del los que participaron al concierto n= 810 durante el festival de 3 días. Cada día intentaba encontrar a todas las personas que censó el primer día. Los valores asignado fueron de 0 a 4 sobre el nivel de limpieza por como olia los participantes

0 = hueles como un cadáver.

4 = hueles a rosas dulces en un fresco día de primavera

library(readr)
DownloadFestival <- read_csv("Data_files_csv/DownloadFestival.csv")



dlf=DownloadFestival  #usamos un nombre más corta para facilitar  
head(dlf) # ver las 3 primeras filas

ticknumb	gender	day1	day2	day3
2.11e+03	Male	2.64	1.35	1.61
2.23e+03	Female	0.97	1.41	0.29
2.34e+03	Male	0.84
2.38e+03	Female	3.03
2.4e+03	Female	0.88	0.08
2.40e+03	Male	0.85

Remover los NA del análisis

Con los datos de los participantes al festival como en algunos diá hay participantes donde no tienen los datos se añadió un NA, es estos casos para que el análisis se logra hay que añadir a la función na.rm=TRUE que significa remover la NA. Para dar se cuenta remueve na.rm=TRUE cuando se usa el “día2” o “día3”, y evalúa que pasa.

mean(dlf$day2, na.rm=TRUE) # na.rm= na remove

## [1] 0.9609091

sd(dlf$day1, na.rm=TRUE)

## [1] 0.9444949

min(dlf$day1, na.rm=TRUE)

## [1] 0.02

max(dlf$day1, na.rm=TRUE)

## [1] 20.02

median(dlf$day1, na.rm=TRUE)

## [1] 1.79

Resumen estadístico de una variable

Para ver los estadístico mencionado arriba (menos la moda, oblicuidad y curtosis) se puede usar la función stat.desc() del paquete pastecs. Para facilitar la lectura de los valores se usa la función “round(x, 3), el tres en esta caso representa la cantidad de valores significativos que se demuestra. Si no usamos round() los valores aparece en notación científicas.

Nota que hay muchos más parámetros calculados. Aparece en la lista en orden el valor mínimo: min(), el valor máximo: max(), la mediana: median, el promedio: mean, la desviación estándar; std.dev entre otros.

library(pastecs)
stat.desc(dlf[,c("day1")])

day1
810
0
0
0.02
20
20
1.45e+03
1.79
1.79
0.0332
0.0651
0.892
0.944
0.527

round(stat.desc(dlf[,c("day1")]), 2)

day1
810
0
0
0.02
20
20
1.45e+03
1.79
1.79
0.03
0.07
0.89
0.94
0.53

Resumen Estadístico de multiples variables

Si uno quiere evaluar múltiples variables continua todas juntos se puede usar la misma función pero el componente c() se añade todas las variables de interés.

round(stat.desc(dlf[,c("day1","day2","day3")], basic=FALSE,norm=TRUE), digits=3) # round reduce a 3 valores significativo

day1	day2	day3
1.79	0.79	0.76
1.79	0.961	0.977
0.033	0.044	0.064
0.065	0.087	0.127
0.892	0.52	0.504
0.944	0.721	0.71
0.527	0.75	0.727
8.83	1.08	1.01
51.4	3.61	2.31
169	0.755	0.595
492	1.26	0.686
0.654	0.908	0.908
0	0	0

Quiz 3: Usa R usa el data.frame Camas_Hospital en el paquete ggversa. Contesta en MSTeam Form con tu respuesta. Selecciona la variable Camas que representa el “número de camas por 1000 personas en muchos países. ¿Cual es el rango (range)?

Los Cuantiles

Los cuantiles son los valores a intervalos específicos de una variable aleatoria continua. Los cuantiles son frecuentemente una mejor interpretación de la distribución cuando los valores no tienen una distribución normal. Típicamente, la distribución se divide en 4 partes con las siguientes partes (los cuantiles 0.25, 0.50 = la mediana, 0.75) y se define como cuartiles. Para meas detalle pueden ver el siguiente enlace https://en.wikipedia.org/wiki/Quantile.

En el siguiente ejemplo se demuestra como tulizar la función quantiles y seleccionar los cuantiles deseados con el comopnente de probs=c(x,x,x).

quantile(dlf$day1,probs=c(0.05, 0.1, 0.25, 0.5, 0.75, 0.95, 0.99), na.rm=TRUE)

##     5%    10%    25%    50%    75%    95%    99% 
## 0.5945 0.8490 1.3125 1.7900 2.2300 2.9100 3.3200

Se puede usar también la función describe en el paquete pshych que le da automáticamente estos cuantiles.

describe(dlf$day1)

vars	n	mean	sd	median	trimmed	mad	min	max	range	skew	kurtosis	se
1	810	1.79	0.944	1.79	1.77	0.697	0.02	20	20	8.83	169	0.0332

El indice de Oblicuidad: Skewness

El indice de oblicuidad es un indice que describe la simetría en una distribución alrededor de su promedio. Otra manera de describirlo es el tercer momento, por que los datos se poner a un exponente elevado al ^3.

La formula es la siguiente. Lo que se darán cuenta es muy similar a la varianza pero note que las diferencias se poner al ^3. Para meas información vea este enlace https://en.wikipedia.org/wiki/Skewness.

\[\frac{1}{N}\sum_{i=}^N\left(\frac{x_i-\overline{x}}{\sigma}\right)^3\]

Primero voy a crear tres conjuntos de datos

con distribución normal
oblicuidad a la izquierda
oblicuidad a la derecha

normal=rnorm(100000, .5, .15)
obliz=rbeta(100000, 1.5,5)
obldr=rbeta(100000, 5.5,2)

normal=as.tibble(normal)

obliz=as.tibble(obliz)

obldr=as.tibble(obldr)

Ahora unimos los data frames y se añade nombres a las columnas

df=cbind(normal, obliz, obldr)
head(df, n=2)

value	value	value
0.359	0.129	0.545
0.665	0.158	0.86

df <- setNames(df, c("normal","obliz","obldr"))

head(df, n=2)

normal	obliz	obldr
0.359	0.129	0.545
0.665	0.158	0.86

El próximo paso es apilar cada columna una sobre la otra. La razón que queremos esto es que deseamos reproducir las variables en un mismo gráfico

library(tidyverse)
df2=df%>%
  gather(key = "Distribución", value="valor", c(normal, obliz, obldr))
head(df2, n=3)

Distribución	valor
normal	0.359
normal	0.665
normal	0.592

# unique(df2$Distribución) # función para ver el nombre de las variables en la columna Distribución

Ahora vamos a ver los datos un gráfico. Vemos que la distribución de los datos son muy diferentes, tanto la distribución en azul y verde están sesgado a unos valores y tienen una cola o valores más grande (azul) o pequeños (verde) que si fuese una distribución normal.

ggplot(df2, (aes(valor, colour=Distribución)))+
  geom_density()+
  xlim(-.01,1)

ggsave("Graficos/Skewness.png")

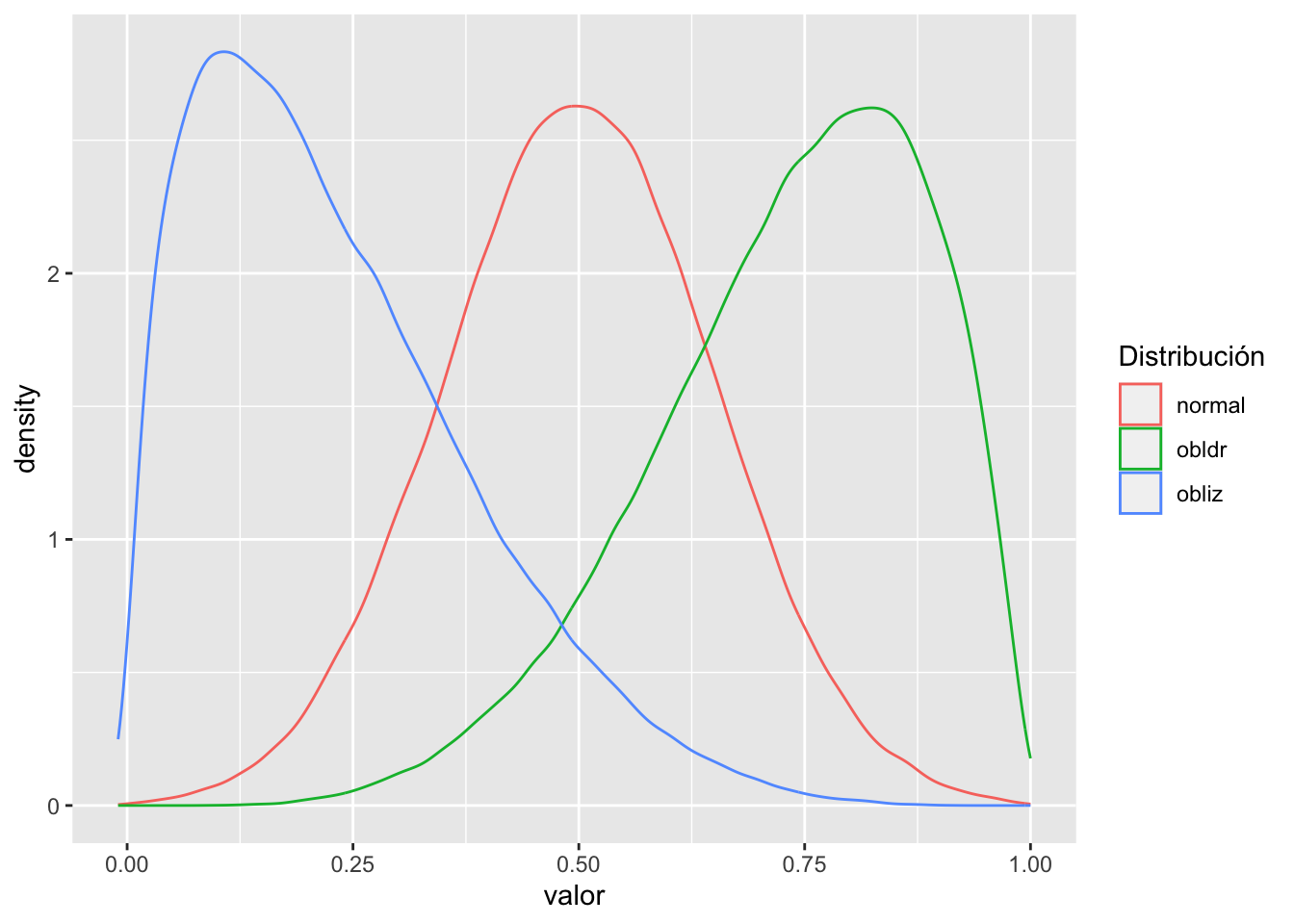
Ahora se calcula el indice de oblicuidad y comparamos los valores. Como regla cuando el nivel de oblicuidad esta entre

-0.5 y 0.5 se considera dentro de una distribución simétrica (normal).
-1.0 y -0.5 o entre 0.5 y 1.o los valores tienen una oblicuidad moderada.
Menor de -1.0 o mayor de 1.0 los datos tienen una oblicuidad grande.

Ahora evaluamos la oblicuidad de los tres gráficos. se usa la función de skewness en el paquete e1071

Para los datos de una distribución normal el valor es muy cerca a cero. Para los datos sesgado a la izquierda el indice de oblicuidad es positivo y el sesgado a derecha es negativo.

library(e1071)
e1071::skewness(normal$value) # la oblicuidad de los datos de una distribución normal

## [1] 0.006368452

e1071::skewness(obliz$value) # la oblicuidad de los datos sesgado a la izquierda

## [1] 0.8262887

e1071::skewness(obldr$value) # la oblicuidad de los datos sesgado a la derecha

## [1] -0.6486796

El indice de Curtosis: Kurtosis

El indice de curtosis es un índice que describe la cola de la una distribución alrededor de su promedio. Otra manera de describirlo es el cuarto momento, por que los datos se poner a un exponente elevado al ^4. El curtosis mide la propensidad de tener daos atípicos.

La formula es la siguiente. Lo que se darán cuenta es muy similar a la varianza pero note que las diferencias se poner al ^4. Para más información vea este enlace https://www.wikiwand.com/en/Kurtosis.

\[\frac{1}{N}\sum_{i=}^N\left(\frac{x_i-\overline{x}}{\sigma}\right)^4\]

Primero voy a crear cuatro conjuntos de datos

con distribución normal
con distribución normal, con cola reducida
con distribución normal, con cola extendida
distribución uniforme

library(PearsonDS)
library(rmutil)

momentsR=c(mean=0, variance=1, skewness=0, kurtosis=2)
momentsE=c(mean=0, variance=1, skewness=0, kurtosis=4)  

normalR=rpearson(100000, moments=momentsR)
normalE=rpearson(100000, moments=momentsE)


Unif=runif(100000, -2,2)
normal=rnorm(100000, 0,1)
laplace=rlaplace(500000, m=0, s=1)


normal=as.tibble(normal)

normalR=as.tibble(normalR)

normalE=as.tibble(normalE)

Unif=as.tibble(Unif)

laplace=as.tibble(laplace)

Ahora unimos los data frames y se añade nombres a las columnas

df=cbind(normal, normalR, normalE, Unif, laplace)
head(df, n=2)

value	value	value	value	value
0.599	1.71	-2.83	1.06	-0.178
-0.538	-1.15	0.22	-1.91	-2.43

df <- setNames(df, c("normal","normalR","normalE", "Unif", "laplace"))

head(df, n=2)

normal	normalR	normalE	Unif	laplace
0.599	1.71	-2.83	1.06	-0.178
-0.538	-1.15	0.22	-1.91	-2.43

El próximo paso es apilar cada columna una sobre la otra. La razón que queremos esto es que deseamos reproducir las variables en un mismo gráfico

library(tidyverse)
df2=df%>%
  gather(key = "Distribución", value="valor", c(normal, normalR, normalE, Unif, laplace))
head(df2, n=3)

Distribución	valor
normal	0.599
normal	-0.538
normal	0.922

# unique(df2$Distribución) #función  para ver el nombre de las variables en la columna Distribución

Ahora vamos a ver los datos en un gráfico. Vemos que la distribución de los datos son muy diferentes, Tiene que concentrar no en el pico de la distribución pero las colas de los datos. Nota la distribución normal que es de color amarillo, y comparar si la colas están por debajo o por encima de esta distribución normal.

Tanto la distribución uniforme (color rosa) y normal reducido (normalR, color azul) las curvas pasan de bajo la curva normal. Al contrarío la linea verde y roja son distribuciones que pasan por encima de la curva normal, entonces las colas son más predominante.

whole=ggplot(df2, (aes(valor, colour=Distribución)))+
  geom_density(adjust=5)+
  xlim(-5,5)

ggsave("Graficos/curtosis_whole.png")


sub=ggplot(df2, (aes(valor, colour=Distribución)))+
  geom_density()+
   theme_bw() +
  scale_x_continuous(limits=c(-5, 1)) + 
  scale_y_continuous(limits=c(0, .1)) +
  theme(legend.position= "none")

ggsave("Graficos/curtosis.png")

sub + annotation_custom(
    ggplotGrob(whole),
    xmin = -1.8, xmax = 1.4, ymin = 0.005, ymax = 0.075)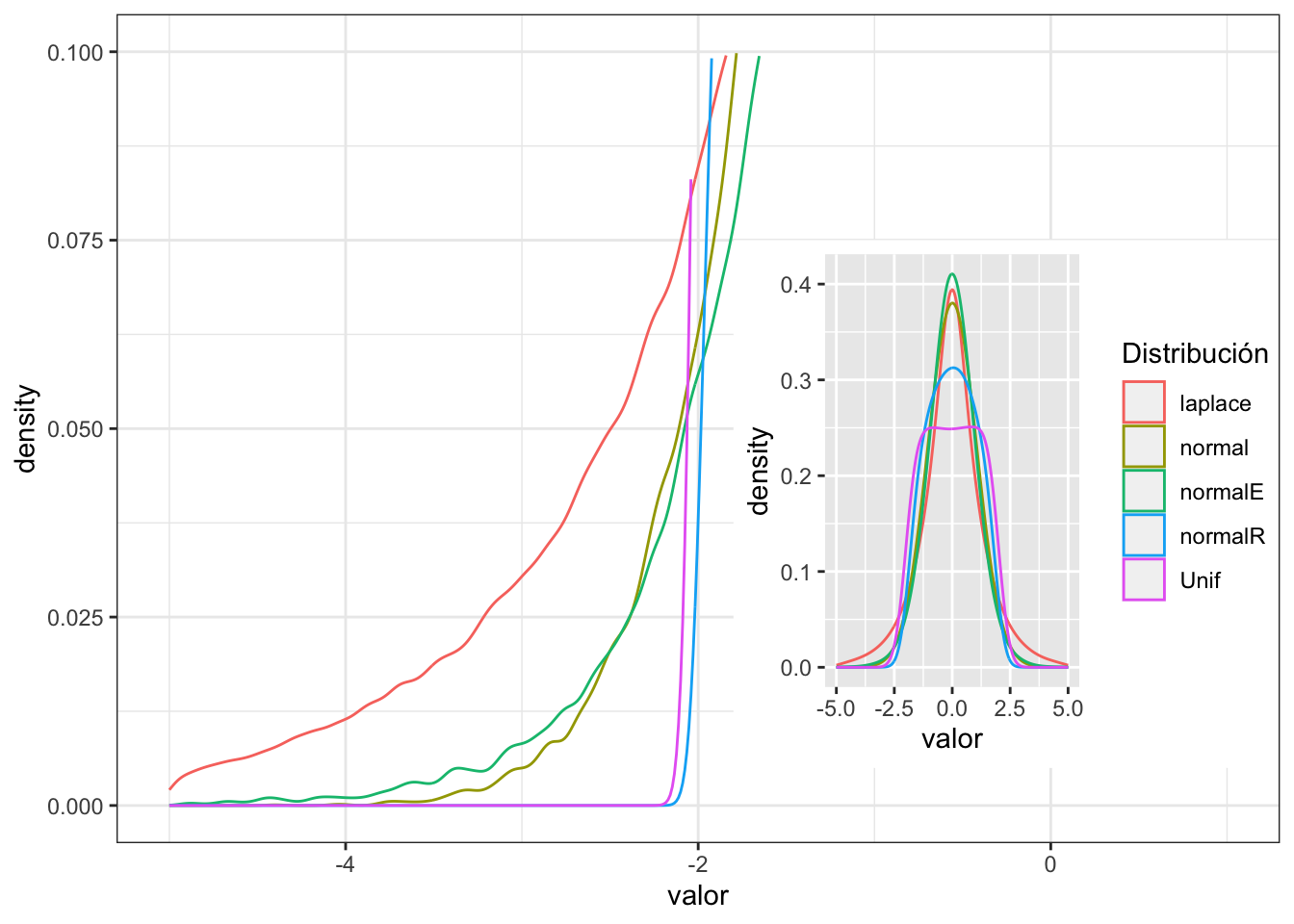

Ahora se calcula el indice de curtosis y comparamos los valores. Como regla el nivel de curtosis esta significativo si los valores de curtosis se enuentra en los siguientes rangos, y se acerca cero no hay curtosis (lo que uno espera para una distribución normal.

Menor de -1.0 los datos están muy aplanados (Uniforme, normalR).
Mayor de 1.0 (la distribución de Laplace).

Ahora evaluamos la oblicuidad de los tres gráficos. se usa la función de kurtosis en el paquete e1071

Para los datos de una distribución normal el valor es muy cerca a cero. Para los datos que tienen exceso de cola el valor de curtosis es negativos y cuando el valor de curtosis es positivo hay exceso de datos en la cola.

library(e1071)
e1071::kurtosis(normal$value) # curtosis de los datos de una distribución normal

## [1] -0.009931754

e1071::kurtosis(normalR$value) # curtosis de los datos restringido

## [1] -1.008095

e1071::kurtosis(normalE$value) # curtosis de los datos con más colas

## [1] 1.142044

e1071::kurtosis(Unif$value) # curtosis de distribución informe, falta de colas

## [1] -1.203061

e1071::kurtosis(laplace$value) # curtosis de distribución Laplace, exceso de colas

## [1] 3.058468

Quiz 1

Quiz 2

Quiz 3

dfNormal=data.frame(data=rnorm(1000000))
head(dfNormal)

data
0.666
1.55
1.05
0.658
1.24
-1.41

ggplot(dfNormal, aes(data))+
  geom_histogram(colour="white", fill="orange")+
  xlim(-4, 4)

ggsave("Normal.png")

T4a_Estadistica_descriptiva