Que es la dispersión en estadística

Las medidas o indices de dispersión, son indicadores de cuan variable los datos son uno del otro. Si todos los valores tienen el mismo valor no hay dispersión. Hay múltiples indices de dispersión vamos a evaluar solamente algunos de estos indices, para más información pueden ir al siguiente enlace https://en.wikipedia.org/wiki/Statistical_dispersion.

Los indices que estaremos estudiando son los siguientes

el rango
la varianza
la desviación estándar
el error estándar
el rango intercuartil
el intervalo de confianza de 95%

Vizualizando la dispersión

Primero miramos un gráfico donde tenemos datos donde el promedio es igual pero la dispersiones son diferentes. Lo que uno observa es que en la distribución azul los datos son más similares uno al otro y la distribución roja los valores son más diferentes. En el primer conjunto de datos se usa 500 valores con un promedio de 100 y una desviación estándar de 10, en el segundo se produce un conjunto de datos de 500 valores con un promedio de 100 y una desviación estándar de 30.

set.seed(8690) # esto es para que los valores se queda igual a cada vez que se corre el analisis
a=rnorm(5000, 100, 10) # la función para generar datos al azar con una distribución normal

dfa=data.frame(a)
dfa

a
122
96.3
97.6
104
87.9
96
95.3
93.1
120
111
107
125
93.9
109
94.6
93.4
104
99.8
116
101
110
101
109
105
79.6
91.7
97.7
89.5
105
93.6
90.4
107
77.4
98.7
108
106
96.7
98.5
105
98.7
102
101
91
88.9
83.7
100
108
101
90.4
102
101
109
108
101
91.7
86.7
101
85.8
109
83.4
98.5
108
89.3
104
98.3
98.6
106
98.8
96.4
92.8
91
99.4
109
107
98.9
113
107
90.7
110
117
89.8
93.8
102
114
90.3
104
88.9
107
113
110
119
112
110
98.2
94.8
101
99.4
109
105
96.4
83.9
93.9
96.6
119
91.5
101
119
88.4
95.3
89.3
99.4
93.8
120
90.4
96.6
116
109
104
104
109
84.3
97.6
98.6
87.3
104
108
89.4
99.6
95.4
119
102
96.9
94.1
108
109
102
87.3
101
105
113
108
85.5
114
118
104
88.9
118
97.5
92.6
86.5
95.5
99.2
99.2
84.1
93.4
106
96.4
105
94.5
95.7
99.1
82.6
92.3
97
105
88.6
114
87.7
115
90.5
95.5
102
102
89.8
96.6
93.3
97.1
123
81.1
94.6
87.6
109
83
75.8
77.2
99.1
117
97.4
102
96.8
103
120
98.3
101
118
109
93
102
108
103
106
110
107
109
95.8
94.4
93.1
103
112
93
96.5
111
106
107
103
101
76.1
111
105
105
107
100
109
93.1
110
104
116
99
98
99.4
104
96.5
100
106
90.3
98.2
95.3
93.1
102
116
97.1
89.9
95.6
84.1
106
105
85.9
104
108
102
84.8
111
88.2
121
87.9
95.6
99.8
87
93.5
104
88.3
91.3
113
102
114
95.7
97.2
92.2
102
83.2
114
107
96
100
93.2
113
107
90.4
104
92.5
96.5
107
103
98.5
106
96.8
109
108
100
104
78.2
120
103
98.7
91.8
97.1
98.4
100
96.3
117
122
104
102
98.8
117
117
90.5
84.5
94.1
97.4
103
102
119
88.3
106
114
119
104
100
113
97.3
105
91.5
104
95.3
106
95.6
101
104
103
111
94.1
101
98.5
100
101
96.9
119
103
102
98.8
106
102
90.8
95.8
116
102
101
114
109
94.3
121
110
89.9
83.5
106
96.4
104
114
121
107
103
87.4
78.8
97
84.4
104
107
103
105
97.2
99.7
102
84.1
105
109
100
97.6
101
97.9
92.9
90.6
99.9
98.3
81.4
102
105
93.9
89.8
96
97.8
88.1
97
112
87.4
82.2
107
117
95.8
101
93.3
102
97.3
105
88.5
108
99.9
104
106
98.3
95.3
92.2
99.9
85.4
96.3
90.9
110
115
117
102
83.4
75.4
103
102
110
114
101
95.4
95.9
95.4
94.1
102
105
99.4
115
85.8
106
91.6
104
95.8
106
90.6
92.8
112
100
107
95.7
97.2
117
98.9
94.1
91
120
94.8
104
109
115
105
101
89.7
75.9
106
97.7
98.2
81.1
110
97.4
105
114
102
85.5
100
103
102
90.2
103
102
75.9
96.7
119
110
88.6
107
118
107
103
102
73
109
92.1
89.7
106
96.1
103
107
106
94.7
96.3
85.9
104
93.5
94
113
108
94.5
96.8
105
115
100
83.6
102
89
96.6
101
116
104
94.2
106
105
99.2
89
90.9
106
106
98.7
116
107
89.2
106
97.8
107
90.3
92.8
78.9
99.8
111
97.8
84.2
116
114
94.7
91.8
89.7
98.5
80.6
88.7
98.1
94.3
105
116
101
107
79.8
104
71.4
91.3
105
106
112
110
97.4
92.6
92.8
88.9
112
111
79.7
89.6
104
99.8
102
81
105
87.1
106
97.3
112
98.8
106
94.4
97.3
104
94.3
105
101
104
87.7
106
79.9
112
101
100
101
98.5
83.5
97.2
100
96
82.1
97.3
103
112
121
96.8
93.5
91.6
104
102
84.4
105
103
94.6
119
92.1
94.8
91.2
99
105
112
116
92.1
97.2
104
97.8
119
93.7
75.6
87
108
98
98.9
105
110
95.8
83.6
88.1
105
92.8
95.5
100
95.3
94.8
133
109
95.8
122
93.8
103
101
89
91
112
97.1
81.9
98.3
93.1
115
101
101
112
112
81.6
101
102
96
93
107
117
95.9
97.5
96.4
82.8
99.2
89.3
82.4
110
95.3
77.8
97.4
92.6
99.6
86.4
90.2
106
115
103
88.9
96.2
97.4
96
101
85.4
126
99.4
82.1
107
91.2
104
103
91.4
90.7
115
102
94.9
96.1
92.1
116
85.7
97.1
104
84.1
76.6
121
99.3
101
102
107
100
99.1
82.7
103
80.7
113
88.6
111
122
89
99.1
97.1
115
107
97.8
108
112
83.8
110
105
100
109
98.7
90.6
96
89.6
106
109
80.2
85.4
110
100
93.9
93.3
115
110
105
84.7
108
81
104
119
98.1
86.4
96.7
117
114
89.8
92
86.7
102
95.5
91.6
102
110
106
77.7
97.1
106
88
100
108
108
115
110
111
83.9
105
106
111
104
96.1
90.8
101
93.8
107
89.5
87.5
92
95.9
106
112
89.6
115
95.5
103
104
103
89.4
103
83.4
113
88
90.3
99.7
94.3
90.5
88
107
103
109
104
96.9
84.4
109
109
106
103
119
89.8
89.1
104
91.6
99.6
100
96.7
88.7
98.8
101
98
94.8
117
108
110
105
102
100
97.7
102
93.4
76.2
98.4
105
103
100
113
92.6
109
109
117
103
104
105
105
78.9
95.5
92.6
104
106
118
97.2
86.3
114
98.3
101
98.9
104
91.6
92.2
89.4
109
86.8
110
123
118
92.8
103
98.1
91.2
98
98.9
99.3
104
88.6
100
100
95.7
99.2
110
112
113
122
92.2
112
98.3
87.2
99.6
105
96.7
83.4
111
115
79.6
105
87.2
101
95.2
101
101
100
97
108
110
101
102
110
86.6
101
115
95.8
101
81.9
105
87.5
110
109
88.1
114
103
91.4
90.3
103
101
102
116
104
95.8
100
98.6
103
83
106
109
98.5
88
108
108
116
109
105
98.5
99.1
120
87.5
84.2
117
117
108
98.7
99
103
113
83.2
120
99
95.3
98.4
103
87.1
93
91.6
95.2
97.6
101
106
118
88.6
96.4
103
123
101
88.2
105
84.3
84.9
97.3
84.2
102
73.8
102
108
115
96.9
115
119
106
92.3
96.3
89.3
104
117
88.5
89.7
105
111
89.9
103
103
86.1
101
103
75.7
102
86.1
109
100
109
108
98.1
104
102
115
102
97.1
102
113
102
96.9
94.5
87.4
90.7
102
84.2
78.8
110
101
87.8
110
103
112
102
105
106
73.5
93.7
103
83.2
105
92.8
110
102
110
94.9
92
97.5
89
95.5
108
111
93
111
87.8
100
103
74.6
81.1
105
110
110
110
104
83.5
112
113
123
96.4
107
108
105
102
92.7
81.2
106
90.4
79.4
110
114
109
92.3
87.9
112
102
94
99.3
109
100
109
87.3
101
119
104
93
94.7
110
89.4
97.8
105
99.1
92.5
116
105
100
98.1
94.5
97.7
114
90.4
93.8
114
109
115
93.9
103
106
111
99
112
109
104
102
97.8
97.6
103
94.2
111
79.7
98.7
108
98.4
97.9
105
96.2
114
107
73.6
100
112
88.2
101
122
99.1
85.2
89.3
98.3
93.3
82.8
98.1
97.1
81.7
93.4
110
108
96.2
108
108
109
82.7
95.3
97.6
95.8
96.8
109
104
116
85.1
94.5
104
111
117
129
89.8
116
94.6
79.6
110
83.5
74.7
98
85.4
72.6
94.1
81.6
96.3
114
87.7
100
102
85.8
107
89.5
105
98.4
94.8
118
96.2
92.7
85
95.7
94.9
98.9
121
99
88.3
102
93.7
103
96.5
94.2
98.5
108
96.8
119
106
93
118
117
93.4
98.4
97
105
97.4
101
75.6
81.2
106
93
97.9
101
99.8
98.3
83.3
103
88.7
124
112
100
86.3
92.9
96.2
108
79.9
116
116
90.4
94.9
98.1
103
94.8
102
88.3
96.8
91.1
104
82.5
110
99.8
111
93.8
106
86.1
97.7
82.7
99.9
85.3
95.6
101
111
79.1
100
89.4
91.4
120
97.9
106
99.5
103
103
102
102
101
101
105
99.3
105
97.5
86.3
97.9
89.6
108
114
86.1
87.8
94.9
89.2
125
95.9
103
109
125
100
94.7
94.7
81.6
101
112
109
104
106
102
102
106
78
120
112
106
100
101
108
94.4
110
113
94.2
98.2
103
106
99.8
99.8
115
88.5
106
98.5
115
107
117
90.3
112
107
81.2
111
97.9
105
103
93
105
106
86.2
105
102
81
97.8
99.7
106
104
90.4
113
109
74.6
110
99.5
91.2
105
91.8
100
87.8
99.6
120
100
111
94.9
84.7
102
88.7
106
103
105
94.8
93.6
108
98.7
110
95.7
110
98
96.9
86.9
90.5
106
88.7
108
108
91.3
83
101
101
103
97.8
108
99.7
101
104
96
105
90
94.8
95.9
105
98.4
102
115
104
93.8
95.1
87.5
93.9
82.5
99.6
104
93.3
121
104
105
108
94.6
105
101
88.2
91.7
103
92.5
104
102
103
104
99.2
93.4
100
92.1
125
107
109
97.8
103
104
111
111
101
96.8
99.6
73.9
86.3
95
118
108
105
99.2
102
112
86
103
105
98.6
100
97.9
98.4
101
82.5
100
110
93.1
89.6
95.2
126
107
92.1
101
105
90.4
88.4
124
107
110
89.2
96.8
101
90.6
95.9
112
96.3
102
104
96.6
88.6
87.3
99.1
104
89.4
86.1
110
81.2
98.1
93.2
84
111
111
125
87.6
89.9
103
98.8
94.7
86.7
107
116
87.5
102
115
96.9
109
102
104
96.2
98.5
85.7
121
108
104
87.1
101
99.8
88
107
112
115
84.6
106
97.4
109
77.1
90.4
92.1
89.9
89.4
104
88.9
99
95.6
95.7
89.6
105
83.9
93.8
94.7
97
87.4
86.9
103
100
113
87.6
113
111
84.8
90.1
87.4
112
96.2
104
120
90.7
96.6
109
96.5
95.6
111
116
86.3
108
85.8
100
97.6
107
104
101
113
93.5
94.1
98.2
82.3
90.1
105
126
104
98.4
91.5
99.8
85.7
96.4
101
90.4
101
104
89.6
90.6
100
95.3
92.2
86.4
80
88.9
112
105
94.8
88.2
74.5
99
93
93.1
93.2
81.1
107
111
84
109
91.1
93
108
93.7
85.9
101
78.6
116
91.7
84.1
88.8
109
108
79.1
111
92.6
95.4
95.8
87.6
101
96.7
99.7
118
95.8
96.1
85.5
109
93.1
93.7
103
96.2
96.1
101
104
112
97.3
113
116
113
98.9
115
113
103
102
106
109
103
114
116
106
89
94.3
104
81.3
86.4
103
80.2
112
110
87.6
100
97.6
99.2
95.2
104
86.8
102
85.9
108
90.9
97
103
89
110
106
84.9
99.1
114
113
85.9
86.5
97.3
89.6
104
113
105
93
108
123
97.9
90.8
110
102
88.8
116
92.9
93
94.9
97.2
93.5
82.9
92.9
104
108
94.2
104
90.1
122
90.6
98
104
113
88.1
87.9
99.8
99.1
108
110
90
67.8
103
111
103
108
108
106
104
102
109
74.3
84.2
93.4
108
116
86.3
121
124
103
95.2
115
96.7
107
113
100
102
101
112
90.3
112
114
113
108
98.8
90.7
102
114
93.6
95.6
99.7
89.6
112
107
99.7
101
76.6
100
93.2
94.5
88.6
93.5
87.2
95
101
109
96.9
89.8
97.4
102
128
97.4
88
113
109
82.8
105
87.5
78.3
113
109
100
115
86.4
109
89.8
82.4
93.5
109
97.9
101
105
92.9
94.5
93.9
71.4
99
115
92.1
106
92.4
102
90.5
88.7
96.9
101
97.9
105
95.4
104
97.6
111
113
99.3
107
102
91.9
92.1
96.5
96.2
88.6
102
117
108
87.3
95.7
98.1
110
99.8
110
113
94.5
95.4
99.1
103
93
115
98.2
100
112
105
97.1
102
98.7
110
105
84.5
92
80.1
116
106
100
90.8
98.8
103
110
93.8
92.9
101
95.7
80.5
109
105
131
93.5
99.5
120
97
95.1
110
115
111
104
98.5
114
114
101
104
106
93
101
105
97.8
93.5
92
85.3
77.6
116
93.2
91.8
92.8
80.9
102
95.9
89.4
90.9
103
106
119
114
81.5
110
95.6
105
99.3
88.9
109
98.9
94.4
88.5
89.8
108
89.5
96.1
95.1
77.1
104
103
97.7
110
121
105
94.6
117
109
93.3
106
96.5
104
117
96.4
96.3
108
90
96.4
111
108
112
107
121
97.1
97.1
86.9
89.6
95.1
108
105
83
104
95.2
107
106
113
89.2
94.9
103
110
102
90.5
119
110
85.7
106
106
107
111
83.4
107
97.6
90.6
99.9
86.9
111
102
99.1
87.4
95.2
86
111
97.2
95.6
112
99
94.9
108
87.9
99.5
102
113
95
105
89.2
85.7
76.2
82.1
118
117
95.8
89.7
95.6
107
104
87.5
87.9
106
109
101
93.3
97.4
101
110
103
95.1
105
85.5
90.7
95
103
90.8
94.7
98.9
96.4
111
81.5
114
89
89.2
108
97.2
134
93.5
102
98.6
99.9
107
98.5
96.2
102
114
110
106
82.7
92.7
85.6
115
104
109
85.4
94.8
108
103
106
115
89.5
117
92.9
103
95.3
113
94.3
108
92.9
92.4
92.5
100
111
108
115
103
91.4
103
103
112
93.8
101
110
109
106
84.9
111
116
96.2
92.4
102
112
106
100
96.8
101
106
111
106
84.9
87.7
122
95.1
101
110
116
109
98.4
103
92.7
119
105
97
91.5
86.5
116
95.7
96.4
102
96.4
119
110
93
83.5
93.9
102
107
93
92.7
119
100
85.8
99.5
98
93.5
93.5
89.2
103
109
96.1
112
95.1
79.6
91.4
94.6
113
101
91.8
90.3
107
84.4
104
102
99
95.6
101
97.9
113
104
108
97.7
108
90.9
94.6
99.3
113
82.9
110
92.6
102
91.2
107
88.2
108
97.6
108
101
104
116
107
93.5
116
111
92.5
95.4
102
82.3
99.9
100
103
85.2
96
108
90.2
87.5
91.8
106
98.1
101
92.5
113
116
96.3
117
104
91.9
93
102
100
106
95.1
111
113
106
109
112
99
92.4
102
94.8
83.8
111
91.8
106
104
90.2
92.1
100
121
102
111
115
97.2
90.4
103
86
89.9
96.6
86.1
93.6
109
107
99.8
102
96.9
103
92.8
109
111
84.1
92.2
105
100
108
90.6
100
109
90.6
99.4
93.3
97.8
97.4
95
116
102
107
109
103
104
98.3
100
100
108
116
107
110
91.2
85.2
104
102
92
91.4
98.3
100
123
88.3
109
93.6
101
114
108
99.6
83.5
90.3
128
117
95.9
100
82.5
98.9
95
113
94.1
102
102
86.1
87.1
114
105
100
93.9
97.1
114
92.5
106
119
90.1
111
102
94.9
85.5
90.5
114
105
100
91.6
94.7
106
95
85.9
107
107
86.9
108
109
82.2
90.8
107
101
101
94.4
92.9
113
120
89.4
97.9
116
92.4
111
85.1
99.2
120
87.5
102
103
94.3
81.4
77.9
84.2
113
89.5
98.7
131
92.3
103
106
98.9
97.5
88.9
97.5
120
95.1
84
94.8
99.6
109
101
98.3
99.8
95
95.1
79.2
100
110
105
86.9
92.8
108
108
96.5
110
80.8
94.6
97.6
94.8
101
97.4
113
114
104
106
99.4
106
82.4
99
86.7
112
100
86.7
116
103
87.3
111
111
112
112
89.6
100
97.3
104
91.8
92.5
115
98.9
110
95.6
103
88.9
97.2
118
103
99.7
109
94.7
94.7
105
99.6
109
101
107
103
106
85.9
82.7
94
88.3
108
109
116
93.1
86.9
82.6
103
100
123
96.9
96
114
119
86.6
94
100
102
86.5
80.3
91
85.5
96.1
85
124
94.3
99.9
95.1
99.1
104
78.9
116
96.7
85.3
94.9
102
112
92.6
101
89.8
106
104
104
96.2
88.3
93.6
90
109
110
91.7
112
105
87.3
83.7
87.1
111
113
104
101
106
102
103
98.1
95.4
88.2
87.5
114
108
108
106
98.9
94.7
77.6
115
98.3
104
94.7
113
101
104
103
96.7
103
97.3
104
103
92.8
131
97.4
100
93.1
109
114
107
79.6
112
106
78.1
88.3
97.5
93.4
79.2
122
93.2
93.5
99.6
96.3
84.2
98.6
92.8
100
123
93.7
101
84.7
95
99.8
91.2
89.7
106
100
83
101
86
87.2
110
106
88.9
122
103
92.1
110
101
98.5
98.3
119
96.1
113
96.8
86
113
110
103
119
103
77.8
105
98
93.2
112
97.2
112
91.9
104
73.5
106
98.2
96.1
73
107
94
97.2
84
131
105
109
94.8
91.1
99.8
97.1
108
95.7
86.5
112
111
104
94
95.6
81
80.8
101
100
99.2
102
98.2
111
113
102
99.2
87.8
106
93
99.5
108
108
97.3
102
108
97.1
99.4
117
115
82.6
107
96.1
100
91.1
85.6
99.9
112
94.3
93.3
116
97.2
94.3
99.2
90.9
93
88.6
101
111
101
110
89.4
100
126
102
85.3
91.2
95.9
109
114
93.7
105
102
84.4
101
101
96.7
106
88.8
93.7
107
99.7
109
91.9
94.7
90.3
97.7
106
90.7
108
84.9
102
106
101
98.3
94.8
95.9
101
110
89.5
107
116
91.5
104
97.1
88.5
86.7
90.7
90.3
85
102
112
103
108
112
87.8
98.3
99.2
97.5
100
98.9
97.7
104
86.6
107
104
104
101
102
94.6
117
95.2
118
101
100
101
105
93.2
105
95.6
88
102
106
125
86.9
102
116
102
99.4
89.2
91.3
92.6
91
90.7
114
84.9
100
98.4
89.4
88.6
93.1
107
101
110
100
104
100
97
80.4
93
99.4
92
105
110
98.6
100
107
92.3
86.6
90.9
114
102
103
111
101
105
90.2
130
110
97.9
104
94.1
84.2
98.8
115
111
102
105
87.8
94.7
112
104
98
107
89.5
95.4
99.4
109
85.2
105
91.2
91.1
110
81.2
91
90.1
99.9
111
103
94.1
100
80
81.9
101
93.2
109
112
98.1
103
117
80.8
102
89.9
90.4
91.5
105
100
97.1
103
94.3
107
101
109
95.3
88.6
95.1
92.3
97.3
117
101
103
89.6
96.9
99.1
87.9
104
112
85.4
83.7
122
106
100
113
109
87.9
100
96.6
111
92.8
84.9
82.7
124
112
85.5
99.3
103
98.7
95.1
116
100
98
112
102
95.6
114
98.4
99.5
101
100
101
108
102
104
87.5
87.6
94
107
105
105
99.8
85.9
101
107
113
93.7
103
109
96.2
86.6
83.6
99.8
98.9
108
93.4
109
119
102
97.1
92.7
100
98.4
97.8
97
99.6
106
111
101
91.8
87.9
93.2
96.1
93.2
95.8
84.2
96
90.4
69.5
70.1
92.9
101
90.3
89.5
102
94.2
93.2
113
104
110
108
105
85.6
83.2
95.4
91
112
107
101
75.1
98.8
99.8
101
95.4
116
102
74.8
94.5
128
95.4
112
104
89.8
103
105
98.5
93.9
96.7
114
97.8
117
101
91.3
91.8
102
97.8
107
99.3
104
106
98.7
94
106
95.4
99.3
101
113
86.5
107
110
89.1
102
111
104
110
105
104
97.6
106
116
79.3
97.1
95.3
98.2
78.9
91.2
101
91.8
111
106
97.2
101
110
98.2
93.8
86.1
118
91.9
101
116
109
89.2
91
92.3
89.4
88.1
102
107
105
108
110
86.6
83.5
97.2
98.7
119
104
100
108
93.6
106
99.5
91.2
94.7
117
108
93.4
111
96.7
97
102
112
99.4
112
89.4
113
104
102
99.6
95.8
120
116
102
107
118
98.6
116
101
112
89.3
96.5
103
89.8
109
95.5
98.1
108
85.8
94.9
92.2
103
97.5
113
86.1
93.6
102
99.7
98.7
106
93
89.8
94
96.2
94
98.3
100
105
98.9
107
110
95.9
96.6
102
98.9
93.3
85
99.4
88.1
105
111
100
107
98.4
92.2
114
96.9
84.8
90
103
91.8
81.3
113
120
85.1
90.5
101
96.1
99.6
102
87.6
112
90.6
112
94.2
105
112
104
90
82.8
97
105
105
122
88.8
106
97.1
94.5
120
96.6
100
98
101
86.5
95.3
108
80
107
109
106
109
107
113
94.4
113
95.4
107
100
79.8
110
107
124
96
121
75.7
112
110
111
107
95.9
105
97.3
99.1
124
104
118
96.7
104
87.9
95.9
92.4
120
95.4
104
100
112
89.2
101
99.3
101
95.3
99.4
95.6
93.7
104
93.4
106
95.8
105
119
107
95.7
92.8
114
95.6
91.2
86.5
103
106
99.2
99.2
104
103
102
98.1
94.5
96.4
101
108
111
96.7
89.3
89.6
118
95.1
105
100
92.4
104
94.2
103
94.8
78.9
102
100
86.9
102
104
106
106
97.2
86.5
104
93.4
110
86.2
98.2
114
79.5
109
118
105
99.4
123
116
96.9
88.4
90.4
87
108
107
106
99.6
93.6
90.1
110
87.5
122
93
100
87.3
84.6
93.6
91.5
103
99
91.2
107
86.4
94
95.8
89.5
125
127
116
95.6
88.5
105
97
100
106
96.1
99.3
97.5
95.5
91.1
93.5
103
95.9
99.1
97.9
98.9
89.6
92.4
121
105
105
91
102
97.5
101
88.5
103
92.1
93.5
100
107
80.6
92.7
91.9
87.6
107
112
115
103
98.3
95.4
82.5
90.6
95.7
100
104
107
92.7
95.8
96.3
89.5
108
104
91.6
108
93.1
103
91.2
99
104
82.6
98.5
93
110
97.7
98.8
98
114
101
104
102
94.9
96
121
88.6
101
122
96.7
91.7
120
112
98.2
111
86
103
93.9
94.7
93.6
96.4
97.2
98.8
102
107
101
98.4
96.3
106
108
96.3
76.9
93.7
94.7
103
94.4
87.9
92.5
109
96.7
125
106
84.4
70.1
97.8
97.3
102
89.1
103
102
102
103
96.5
93.9
101
87.9
105
77.8
100
97.8
78.6
98.4
102
92.1
86.9
113
99.7
102
89.6
94.2
114
114
114
76.6
111
76.7
102
110
97.8
103
99.8
119
110
84.9
102
95.1
102
105
100
107
91.8
110
96.4
117
86.1
92.8
113
90.3
98.7
91.2
97.6
92.3
103
92.3
88
98.4
103
101
97
103
106
90.3
98.3
101
89.6
116
108
102
89.5
101
105
92.5
99.7
110
98.8
106
89.4
106
95.9
100
100
106
120
102
94.2
102
98.6
120
86.7
122
108
109
109
101
83.4
102
85.4
94
95.2
105
88
90.1
103
106
112
95.5
117
110
91.2
98.7
103
85.6
103
101
104
90.1
107
101
84.9
104
83.5
98.5
118
119
95.4
77.1
116
95.8
81.2
91.9
102
87.7
110
107
89.8
98.8
108
114
101
96.2
94.2
93
93.7
109
82
109
116
104
87.1
92.4
87.1
74.3
111
114
102
120
99.8
100
107
96.5
119
88.7
109
102
107
97.4
80.5
96.7
104
96.1
95.8
108
108
104
91.5
102
115
109
134
93.6
111
98.2
81.5
114
102
92.2
87.8
94.2
108
107
103
98.7
91.9
98.7
103
106
95
112
98.4
89.1
81.2
102
91.4
96.7
96.4
87.3
94.5
111
97.1
93.9
107
102
102
90.2
90.2
90.9
105
112
99.6
103
106
83.5
98.4
123
104
85.5
119
117
89.5
92.4
91.6
107
95.5
106
112
92.4
103
88.1
91.5
76.8
88.5
101
112
110
99.1
93.8
103
95
109
103
113
103
96.9
92.6
108
94.3
106
95.8
104
88.9
124
90.2
104
92.7
103
106
81.3
77.4
115
103
103
79.2
100
111
93
103
117
90.8
103
82
106
90.8
101
95.9
94.6
100
89.4
104
107
117
101
107
104
111
107
109
109
103
92.4
100
95.5
111
120
88.3
102
94.3
84.7
94.6
95
84.8
94.1
100
110
101
109
120
106
83.2
107
87.2
109
88.2
114
97.4
81.4
104
98.5
108
105
119
107
98.7
91.8
88.8
108
98.9
108
91.4
84.4
111
87.8
110
101
89.7
105
106
99
96.4
116
113
119
96.9
104
95.8
104
93.6
101
94
85.8
99.7
95
111
87.6
102
94.1
122
84.1
94
81.9
114
101
98.2
92.8
104
105
103
101
101
94.7
87.6
92.5
95.1
92.5
103
86.4
105
96.1
89.2
97.6
80.8
110
99.7
95.1
117
89.3
103
85.4
86.9
81.7
93.9
89.5
93.2
109
116
97.1
88
79.1
84.4
102
97.4
109
108
106
97.2
92.6
113
101
108
103
102
98.3
96.2
94.7
91.3
105
105
103
67.8
95.8
100
116
97.9
102
94.7
117
106
92.6
113
93
85.7
108
94.7
95.6
105
107
110
97.9
97.9
103
88.3
118
110
110
97.4
96.2
108
124
89.6
96.8
118
102
129
109
90
110
111
91.5
105
98.1
99.5
126
102
87.6
114
111
88.6
91.6
105
83.5
110
109
94.1
96
85.9
76.3
101
103
91.2
109
107
75.5
95.9
115
112
101
109
104
95.7
95.5
111
97.1
117
94.3
114
97.9
108
89.3
92.3
94.1
103
100
96.2
85.1
99.7
102
94.4
93.2
108
116
99.4
115
93.9
105
95.9
97.5
98.4
92.9
98.7
109
88
107
99.4
96.7
79.9
93.4
114
90.4
88.5
108
95.4
118
88.7
102
101
88.6
103
97.9
101
99.8
101
110
97.5
114
82.4
97.3
91.5
87.6
83.1
85
113
99.7
99.9
86.3
88.7
105
93.3
92.3
97.6
102
98.9
93.7
113
101
99.8
102
89.4
89.3
123
94.2
121
99.5
101
109
81
115
91.8
91.1
104
103
105
94.4
99.7
111
116
116
104
87.5
96.1
97.4
102
96.9
101
98.2
102
105
99.3
118
99.1
103
96.1
115
103
97.8
113
97.2
99.2
94.8
102
86.1
107
118
108
102
94
99
92.5
88.9
102
93.5
98.3
116
93.4
113
105
117
105
97.3
104
100
105
85.6
87.6
109
93.2
84.8
79.4
108
96.4
124
89.7
93.7
88.1
115
96.4
101
99.3
85.4
117
108
101
116
103
108
95.9
117
93
99.4
87.4
73
104
103
105
84.3
106
99.1
107
111
90.3
100
112
97.5
103
102
97.5
107
107
101
105
95.8
103
96.2
113
113
95.2
111
101
105
86.6
105
111
104
83.3
111
92.1
109
107
115
123
100
106
97.5
106
86.5
112
103
112
126
102
85.6
109
91.8
111
113
97.5
97.7
91.6
108
117
107
98.4
80.5
105
105
91.3
87.4
104
101
104
115
106
91.7
105
104
80.6
112
107
108
84.9
92.8
118
98
88.7
106
94.8
104
89.5
82.6
114
94.7
94.9
114
91.4
93.2
105
101
93.7
115
114
92.3
106
98.9
89.9
102
116
91.3
116
100
99.6
95.5
79.4
104
103
96.6
96.3
87.5
100
86.5
94.1
98.1
128
83.4
99.9
101
91
107
82.6
94.7
94.3
101
101
114
102
95.9
95.9
101
91.3
92.3
105
101
94.6
96.1
99.9
101
98.1
101
104
100
102
92
97.1
108
96.3
100
103
112
101
96.4
113
92.8
97.5
89
94.4
105
117
102
115
105
91.5
97.3
88
115
86.1
108
107
100
96.5
110
93.2
99.4
86.2
105
93.8
88.7
98.6
106
109
100
90.9
94.1
91.8
98.9
91.4
99
97.9
102
101
105
105
101
105
124
109
102
98.8
110
88.6
102
102
105
92.4
87.1
96.3
96.2
97.6
93.3
102
97.7
102
104
117
102
103
107
101
104
114
93.2
75.2
118
103
78.9
106
92.3
85.3
91.6
111
109
91.4
123
103
95
115
106
102
102
118
116
95.8
94.9
95.7
89.5
106
94.8
117
90.6
98.4
96.3
99.8
92
96.5
95.2
101
80.9
109
97.9
90.3
113
88.9
95.8
77.7
95.2
85.4
103
106
117
113
124
96.8
109
103
94.2
82.9
87.9
99.2
116
98.3
85.3
88.9
119
87
119
103
108
95.8
102
93.4
97.5
96.1
102
100
101
80.5
102
97.4
104
99.5
105
110
120
99.7
86.1
92.2
113
95.8
80.9
106
91.6
87.1
94.8
111
101
109
97.5
96.7
99.1
115
98.4
99.6
100
92.5
106
132
110
108
89.9
92.5
103
121
91.3
117
96.9
112
87.8
95.2
118
99.5
106
108
104
95.8
87.8
105
80.3
96.6
117
105
107
99.7
103
88.2
99.6
98.2
85.6
90.8
102
109
110
109
111
98.2
116
90.4
98.7
107
88.8
97.4
112
112
95.1
88.6
99
81.3
111
110
119
102
93.3
102
114
115
94.3
104
91.4
95.4
104
103
114
109
112
101
91.4
105
115
83
109
110
92.2
103
105
87.7
117
91.1
74.9
100
86.8
100
88.1
93.8
102
103
118
94.4
108
97.7
84.4
95.5
125
104
92.8
91.1
89.3
99.3
92.5
87.9
108
88.8
112
98.7
99.3
103
108
96
87.4
116
105
95.9
85.9
81.8
106
92.7
80.4
102
99.3
79.4
106
105
102
105
111
100
98.9
98.3
99.3
98.6
74
102
121
95.9
102
88
89.3
94
102
100
93.9
103
100
104
106
90.7
132
99
88
101
105
101
95
98.8
116
116
91
95.2
101
92.3
102
117
98.4
99.9
89.7
111
104
104
108
94.4
106
117
118
108
117
116
104
102
98.3
88.3
91.8
112
98
94
100
90.6
96.1
102
105
85.9
88.7
93.8
88.9
94.1
105
77.9
95.5
107
95.3
91.8
110
101
80.3
109
108
107
114
97.3
108
92.6
95.9
112
93.3
103
111
108
97
99.8
107
110
103
89.4
101
90.3
89.7
100
89.4
97.7
100
93.4
98.2
85.4
86.4
104
120
103
88.7
104
94.6
102
106
107
106
101
91.5
96.2
104
109
98.6
95
101
111
121
117
107
111
106
118
108
95.8
115
110
102
111
101
106
92.2
113
93
97.1
92.5
97.1
87
104
100
95.1
113
102
96
111
99.7
92.7
97.9
95.1
109
101
92.7
114
101
97.8
95.3
127
108
99.9
78.8
101
94.6
77.7
86.7
115
100
111
122
96.2
107
90
106
111
104
117
105
92.9
87.6
89.7
115
107
103
86.3
98.1
103
116
118
102
100
94.3
92.4
117
117
88.4
116
113
82.1
95.9
91.9
95.7
111
104
104
113
81.3
92
106
103
91.1
98.8
91.6
101
86.3
104
88.9
107
88.9
87.8
101
91.8
92
102
82.5
83.6
105
97.6
101
109
93.9
87.9
92.4
91.3
106
113
95.3
109
96.7
116
105
103
108
84.3
94.2
117
97.5
113
97.6
95.7
99.6
103
103
121
104
97.3
88.7
101
95.3
109
97.1
112
114
119
111
116
132
105
99.5
101
96.7
97.9
105
110
102
87.3
91.7
82.1
93.4
97.5
98
119
96.1
85.6
95.1
84.1
95.5
92.8
86.3
89.7
117
107
106
117
89.5
93.6
91.4
90.9
94.2
104
78
101
107
108
124
109
92.8
99
99.4
106
91.8
113
104
118
102
118
94.5
104
85.3
110
75.6
102
99.7
113
75.1
97
107
115
125
102
79.4
102
106
114
100
97.8
99.2
97
89.6
99.9
113
111
90
107
91
89.8
105
109
85.2
82.1
95.7
102
88.4
99.8
106
95.8
85.9
96.8
118
114
115
93.7
86.4
111
97.2
88.8
96.8
95.4
97.8
107
97
103
99.7
108
104
108
98.1
95.6
101
97.1
91.9
105
106
88.2
89.8
96.9
112
94
107
108
115
88.5
113
123

 # r is for random
 # norm =distribución normal
#a
b=rnorm(500, 100, 50)
dfb=data.frame(b)

library(ggplot2)

ggplot(dfa, aes(a))+
  geom_density(fill="blue")+
  geom_density(dfb, mapping=aes(b,fill="red", alpha=.5 ))+
  theme(legend.position = "none") +
  geom_vline(aes(xintercept = 100, colour="red"))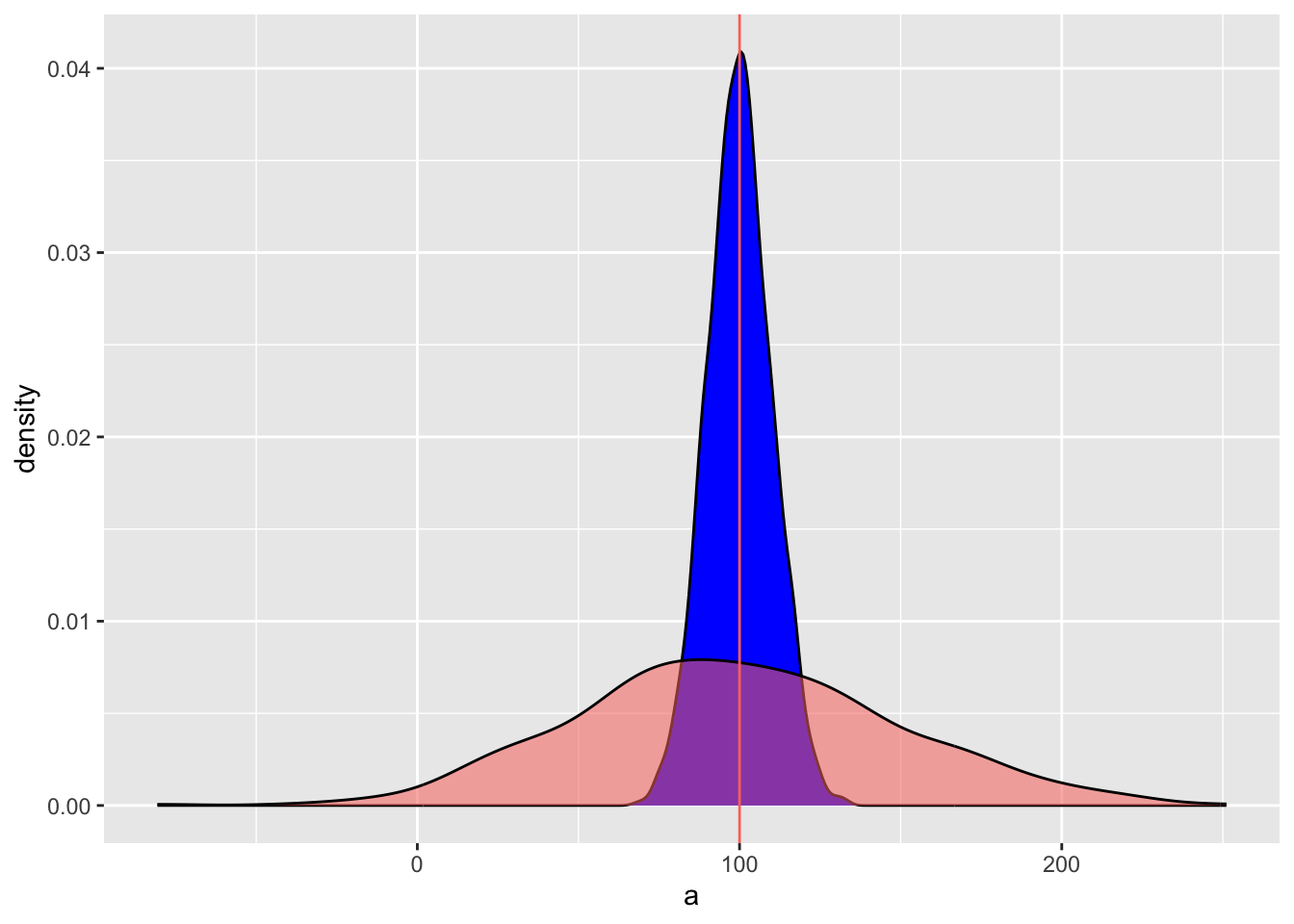

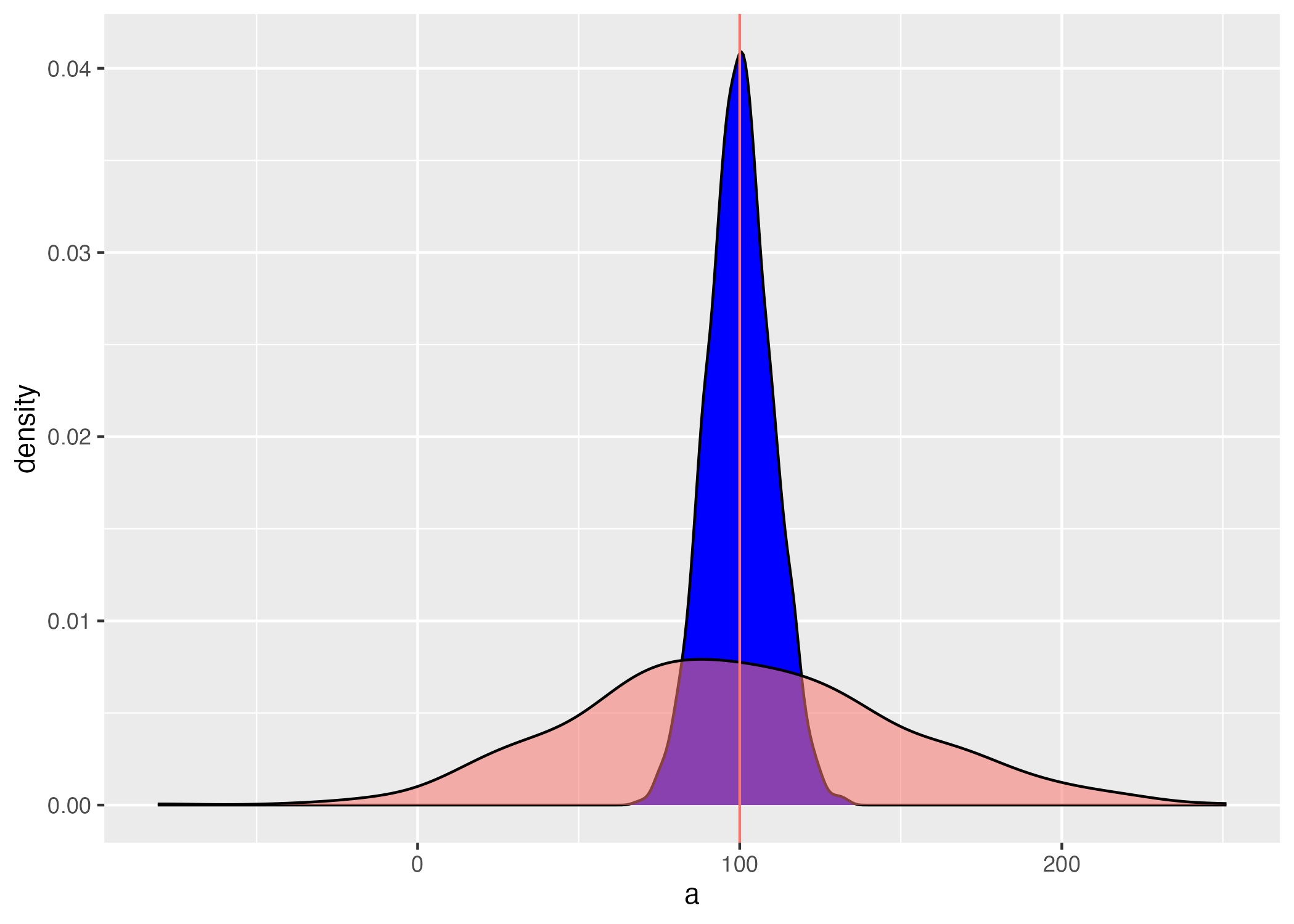
ggsave("Graficos/dispersion.png")

El rango

El rango son los valores mínimo y valor máximo de un conjunto de datos. Se usa la función range(). Usamos los dos conjuntos de datos ya creado anteriormente para visualizar los rangos de la distribuciones de los gráficos. Lo que uno observa es que el valor mínimo del primer conjunto de datos es 59.17 y el máximo es 137.12. Para el segundo conjunto de datos el valor mínimo es 1.86 y el máximo es 203.88.

range(dfa$a)

## [1]  67.77126 133.87095

range(dfb$b)

## [1] -80.68499 251.11763

Ejemplo de la clase

Cual es el rango de la Edad de los padres de los Estudiantes

Edad=c(57,50,43,39,54,50,59,49, 57,51,43,47)
Edad

##  [1] 57 50 43 39 54 50 59 49 57 51 43 47

Edad_df=data.frame(Edad)
Edad_df

Edad
57
50
43
39
54
50
59
49
57
51
43
47

range(Edad)

## [1] 39 59

range(Edad_df$Edad)

## [1] 39 59

Dist_V=c(14, 71, 16, 43, 32, 17.1, 11, 53, 16.2, 47, 18.2, 39, 9, 16.2)

df=data.frame(Dist_V) # para poner los datos un un data frame

df

Dist_V
14
71
16
43
32
17.1
11
53
16.2
47
18.2
39
9
16.2

Caluclar la varianza

var(df$Dist_V)

## [1] 359.3963

Desviación estandard

sd(df$Dist_V)

## [1] 18.95775

Error estandard

error_e= sd(df$Dist_V)/sqrt(length(df$Dist_V))
error_e

## [1] 5.066672

95% de la distribución

Limite_inferior_a=mean(df$Dist_V)-(error_e*1.96)

Limite_superior_a=mean(df$Dist_V)+(error_e*1.96)


Limite_inferior_a

## [1] 18.83361

Limite_superior_a

## [1] 38.69496

La varianza

Los pasos para calcular la varianza son los siguientes

tener un conjunto de datos, aquí lo llamamos Data
convertir esta lista en un data frame
Calcular el promedio de los datos
restar el promedio de cada valor y cuadralos
Sumar y restas de n-1, done n es la cantidad de datos
el numerador se llama la suma de los cuadrados = SS

\[{ s }^{ 2 }=\frac { \sum { { ({ x }_{ i }-\bar { x } })^{ 2 } } }{ n-1 }=\frac{SS}{n-1}\]

library(tidyverse)
Data=c(1,2,3,4,5,6)
Data_df=data.frame(Data)
Data_df

Data
1
2
3
4
5
6

Data_df$mean_Data=mean(Data)   # Aqui se añade el promedio a cada fila
Data_df

Data	mean_Data
1	3.5
2	3.5
3	3.5
4	3.5
5	3.5
6	3.5

Data_df$Diff=Data_df$Data-Data_df$mean_Data 
          # Calcular la diferencia entre el promedio y el valor x
sum(Data_df$Diff) # si los valores no se cuadra la suma sera zero.

## [1] 0

Data_df$SS=(Data_df$Data-Data_df$mean_Data)^2 # SS para la suma de los cuadrados 
Data_df

Data	mean_Data	Diff	SS
1	3.5	-2.5	6.25
2	3.5	-1.5	2.25
3	3.5	-0.5	0.25
4	3.5	0.5	0.25
5	3.5	1.5	2.25
6	3.5	2.5	6.25

sum(Data_df$SS)

## [1] 17.5

### Este indice se llama la desviación del promedio que es la suma de los cuadrados

Calcular la varianza con var()

Ahora la manera fácil de hacer los análisis, usar la función var, y no hay que hacer ninguno de los pasos anteriores. Pero es importante que sepa como es el procedimiento de calcular la varianza. Nota que la varianza es un indice de la diferencia entre el promedio y cada valor. El otro paso es que los valores tienen que estar cuadrada las diferencias sino la suma sera de cero. Se usa el variancas cuando tenemos confianzas que los datos provienen de una distribución normal y que los datos que uno tiene no están sesgados.

var(Data)

## [1] 3.5

La desviación estandar

La varianza es un indice que no esta en la misma unidad que los valores recolectado, por ejemplo si se recolecta los datos en centímetros, la varianza es en centímetros cuadrados. Por consecuencia no es necesariamente el mejor para describir la dispersión. Entonces hay que sacar la raíz cuadra de la varianza. La desviación estándar es un indice que se usa para describir la dispersión de una población, en otra palabra cuan diferentes son los datos uno del otro. Se usa el desviación estándar cuando tenemos confianzas que los datos provienen de una distribución normal y que los datos que uno tiene no están sesgados.

\[{ s }=\sqrt { \frac { \sum { { ({ x }_{ i }-\bar { x } })^{ 2 } } }{ n-1 } }\] o más sencillo

\[s=\sqrt{s^2}\]

la función sd, “standard deviation” es sumamente facil de calcular en R.

sd(Data_df$Data)  # deviación estandard

## [1] 1.870829

El rango intertcuartil.

La función básica es quantile si lo dejamos sin más instrucción calcula los siguientes probabilidades 0%, 25%, 50% (mediana), 75%, 100%. Pero si uno quiere los valores que se encuentra en una posición especifica hay que usar type =1 como se ve en el segundo ejemplo. Hay 9 tipos de cuantiles con esta función, estos se encuentra definido en RStudio. Añade quantile en el artea de help y vera las otras alternativas.

quantile(Data) # la función básica (0%, 25%, 50% (mediana), 75%, 100%)

##   0%  25%  50%  75% 100% 
## 1.00 2.25 3.50 4.75 6.00

# Seleccionar los cuantiles específicos.
quantile(Data, probs = c(0.025, 0.25, 0.50,.75, .975))

##  2.5%   25%   50%   75% 97.5% 
## 1.125 2.250 3.500 4.750 5.875

Para explicar estos conceptos mejor visualizamos los datos

i	x[i]	Mediana	Cuartiles
1	03
2	19
3	27
4	33		Q1=33
5	52
6	60
7	77
8	87	Q2=87
9	99
10	101
11	122
12	137		Q3=137
13	140
14	142
15	150

Ahora usamos la función quantile con el type=1 de calcular los cuartiles y ver si tenemos los mismos resultados.

dat=c(3,19,27,33,52,60,77,87,99,101,122,137,140,142,150)

quantile(dat, type =1)

##   0%  25%  50%  75% 100% 
##    3   33   87  137  150

sd(dat)

## [1] 49.2145

El error estandard

El termino correcto es el error de las desviación estándar pero típicamente acortado a error estándar. El indice de error estándar es para describir cual es la posible dispersión del promedio. En otra palabra cuan confiado estamos con el estimado del promedio. Más grande el error estándar menos confiado estamos con el promedio. Se usa el error estándar cuando tenemos confianzas que los datos provienen de una distribución normal y que los datos que uno tiene no están sesgados.

La formula de error estándar es la siguiente usando la desviación estándar

\[s_{\overline{x}}=\frac{s}{\sqrt{n}}\]

o usando la varianza, donde la n es la cantidad de datos

\[s_{\overline{x}}=\sqrt{\frac{s^2}{n}}\]

Ahora si usamos los datos enseñado al principio del modulo. Calculamos error estándar de ambas distribución. er= error estándar. No hay función en R para calcular el error estándar, por consecuencia hay que crear la formula para calcular el indice. Vemos que cuando hay más dispersión el error estándar es más grande.

length(dfa$a)

## [1] 5000

es_a= sd(dfa$a)/sqrt(length(dfa$a))

es_b= sd(dfb$b)/sqrt(length(dfb$b))

es_a

## [1] 0.1405601

es_b

## [1] 2.204251

El intervalo de confianza de 95% del promedio

Ya que hemos calculado el error estándar podemos calcular la dispersión de los promedios. Esto quiere decir que si uno repite la recolección de datos el promedio tiene un 95% de probabilidad estar en este rango. Uno calcula los limites de la dispersión de los promedios usando la siguientes formulas.

\[Limite\ 95\%\ ariba=\ \overline{x}\ +\left(ES\ \cdot\ 1.96\right)\]

\[Limite\ 95\%\ abajo=\ \overline{x}\ -\left(ES\ \cdot\ 1.96\right)\]

Limite_inferior_a=mean(dfa$a)-(es_a*1.96)

Limite_superior_a=mean(dfa$a)+(es_a*1.96)

Limite_inferior_a # limite inferior 95%

## [1] 99.73334

mean(dfa$a)   # El promedio

## [1] 100.0088

Limite_superior_a # el limite superior 95%

## [1] 100.2843

Limite_inferior_b=mean(dfb$b)-(es_b*1.96)
Limite_superior_b=mean(dfb$b)+(es_b*1.96)

mean_b=mean(dfb$b)
Limite_inferior_b

## [1] 94.81576

mean(dfb$b)

## [1] 99.13609

Limite_superior_b

## [1] 103.4564

Visualizando el intervalos de confianza del promedio. Lo que uno observa es que primero el promedio puede ser en localidad diferentes porque el conjunto de datos fue menos en el segundo gráfico. Además vemos que el intervalo de 95% de confianza del promedio en el segundo es más amplio.

CI_a1=ggplot(dfa, aes(a))+
  geom_histogram(fill="blue", colour="white",alpha=.5, binwidth = 2)+
  theme(legend.position = "none") +
  geom_vline(aes(xintercept = 100), colour="red")+
  geom_vline(aes(xintercept = Limite_inferior_a), colour="black")+
  geom_vline(aes(xintercept = Limite_superior_a), colour="black")
ggsave("Graficos/CI_a1.png")

CI_b=ggplot(dfb, aes(b))+
  geom_histogram(fill="blue", colour="white", alpha=.5, binwidth = 5)+
  theme(legend.position = "none") +
  geom_vline(aes(xintercept =mean_b), colour="red")+
  geom_vline(aes(xintercept = Limite_inferior_b), colour="black")+
  geom_vline(aes(xintercept = Limite_superior_b), colour="black")


ggsave("Graficos/CI_b.png")

#library(easyGgplot2)
#ggplot2.multiplot(CI_b.png,CI_b.png, cols=2)

El intervalos de confianza de los datos

Para tener una idea de la distribución de los datos y cual es el porcentaje de valores que esté incluido (asumiendo una distribución normal). Podemos crear un gráfico que demuestra el porcentaje incluidos basado en la desviación estándar. Nota aquí no es la dispersión del promedio pero la dispersión de los datos en la población.

Rangos incluidos en intervalos de confianza

Cálculos el promedio y la desviación estándar de los datos. Lo haremos por genero. Si uno calcula el rango de promedio ± 1 sd, esto incluye 68.2% de los datos, si incluimos el promedio ± 2 sd incluye 95.6% de los datos,

Rangos incluidos en intervalos de confianza
sd	rango inluido
0	el promedio
±1	68.2%
±2	95.6%
±3	99.7%
±4	99.99%

Ejemplo del intervalo de confianza

El intervalo de confianza de colesterol en los Iranis

Comenzamos con evaluar el intervalo de confianza de los datos con datos teóricos. Por ejemplo el nivel de colesterol en el plasma varia en los humanos. En el siguiente articulo Plasma total cholesterol level and some related factors in northern Iranian people. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3783780/

Usamos los datos para las mujeres con un promedio de 196.7 y una desviación estándar de 39.11. Con estos datos asumimos que esto provienen de una distribución normal y que representa las mujeres en resto del mundo.

# Creamos un conjunto de datos para los análisis

Col=rnorm(200000, 196.7, 39.11)
Col=data.frame(Col)

promCol=Col%>%
  summarise(Mean=mean(Col))
  
sdCol=Col%>%
  summarise(sd=sd(Col))

Visualizar los datos: Uds conoce su nivel de colesterol total? Donde se encuentra en esta distribución? Se encuentra en el 68%? Nota que la suma de todos los porcentaje es igual a 100%.

library(grid)
library(gtable)

lims <- c(28, 350)

breaks.major2<-c(0, 79, 118, 157, 
                 197, 235, 274, 314)
breaks.minor2= c(79, 118, 157,197, 
                235, 274, 314,379)
breaks.comb <- sort(c(breaks.major2, breaks.minor2-1.0E-6))
labels.comb<- c(0, 79, "\n-3sd", 118, "\n-2sd", 157, "\n-1sd", 197, "\npromedio",
                 235,  "\n+1sd",274, "\n+2sd", 314,"\n+3sd", 379)

Colesterol_Inter=Col%>%
ggplot(aes(Col))+
  geom_histogram(fill="blue", colour="white",alpha=.5, binwidth = 5)+
  theme(legend.position = "none")+
  geom_vline(xintercept=as.numeric(promCol), colour="black")+
  geom_vline(aes(xintercept = as.numeric(promCol-sdCol)), colour="blue")+
  geom_vline(aes(xintercept = as.numeric(promCol+sdCol)), colour="blue")+
geom_vline(aes(xintercept = as.numeric(promCol-2*sdCol)), colour="red")+
  geom_vline(aes(xintercept = as.numeric(promCol+2*sdCol)), colour="red")+
geom_vline(aes(xintercept = as.numeric(promCol-3*sdCol)), colour="orange")+
  geom_vline(aes(xintercept = as.numeric(promCol+3*sdCol)), colour="orange")+
  scale_x_continuous(expand=c(0,0), limit=lims, 
                                minor_breaks=breaks.minor2, 
                                breaks=breaks.comb,
                                labels=labels.comb)+
  xlab("Nivel de colesterol")+
  annotate("text", x=180, y = .004, label="34.1%")+
  annotate("text", x=210, y = .004, label="34.1%")+
  annotate("text", x=140, y = .002, label="13.6%")+
  annotate("text", x=250, y = .002, label="13.6%")+
  annotate("text", x=90, y = .001, label="2.1%")+
  annotate("text", x=295, y = .001, label="2.1%")+
  annotate("text", x=70, y = .0005, label="0.1%")+
  annotate("text", x=330, y = .0005, label="0.1%")
Colesterol_Inter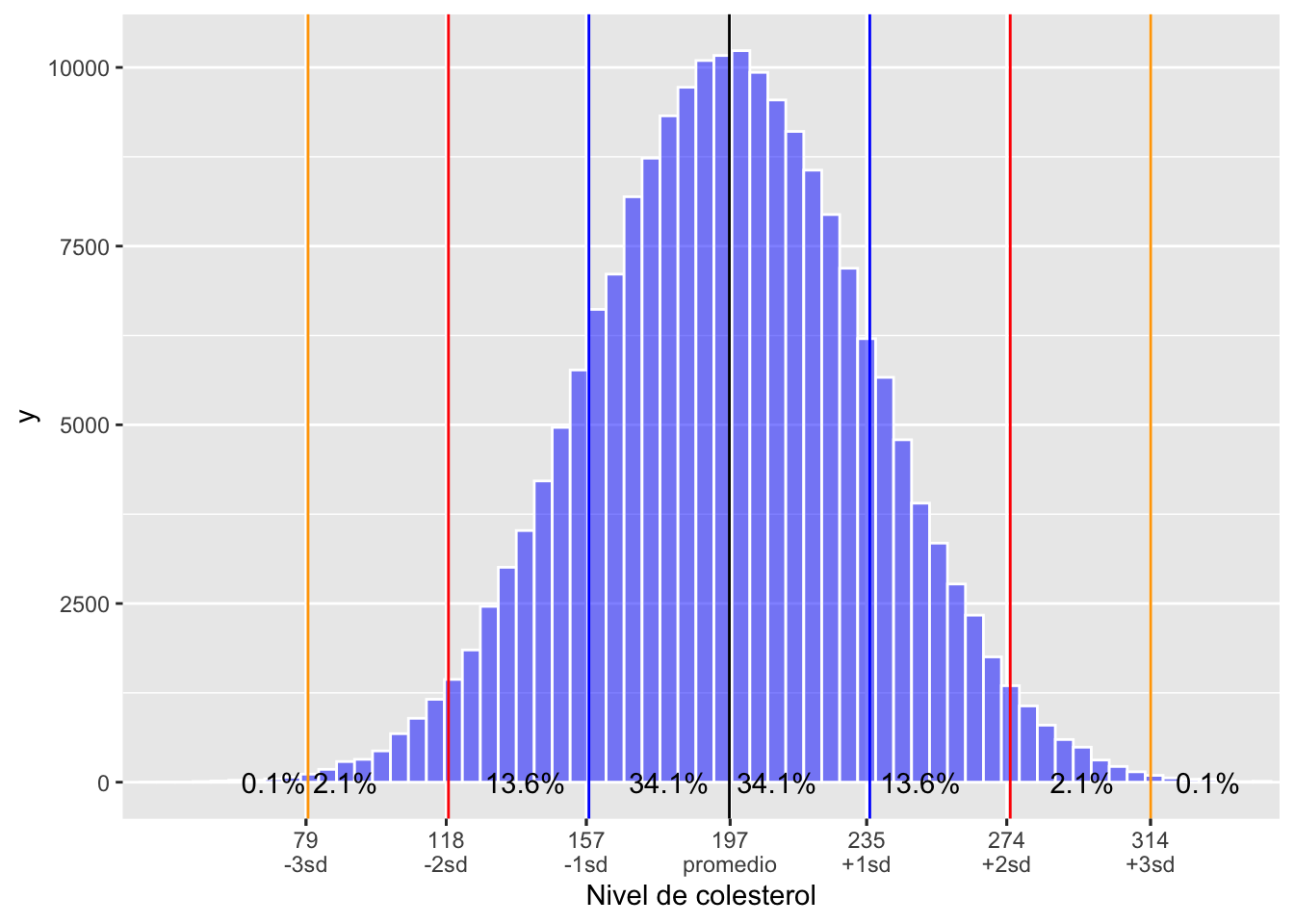

ggsave("Graficos/Colesterol_Inter.png")

Otro ejemplo de los intevalos de confianzas

La altura de los humanos

Para evaluar el 95% de intervalo de confianza usaremos datos de la alturas de 500 adultos. Estos datos fueron bajado del siguiente website. Están disponible en debajo la pestaña de “Los Datos”. https://www.kaggle.com/yersever/500-person-gender-height-weight-bodymassindex/data

library(readr)
library(gt)
Alturas_Humanos <- read_csv("Data_files_csv/Alturas_Humanos.csv")
gt(head(Alturas_Humanos))

Genero	Altura_cm	Peso_kg
Hombres	174	96
Hombres	189	87
Mujer	185	110
Mujer	195	104
Hombres	149	61
Hombres	189	104

Calculamos los promedios y las desviación estándar para añadirlos al gráfico

library(tidyverse)
head(Alturas_Humanos)

Genero	Altura_cm	Peso_kg
Hombres	174	96
Hombres	189	87
Mujer	185	110
Mujer	195	104
Hombres	149	61
Hombres	189	104

length(Alturas_Humanos$Genero)

## [1] 500

# Parametros para las Mujeres
promM=Alturas_Humanos%>%
  dplyr::select(Genero, Altura_cm)%>%
  filter(Genero=="Mujer")%>%
  summarise(MeanM=mean(Altura_cm))
promM

MeanM
170

sdM=Alturas_Humanos%>%
  dplyr::select(Genero, Altura_cm)%>%
  filter(Genero=="Mujer")%>%
  summarise(sd=sd(Altura_cm))
 sdM

sd
15.7

# Parametros para las Hombres
promH=Alturas_Humanos%>%
  dplyr::select(Genero, Altura_cm)%>%
  filter(Genero=="Hombres")%>%
  summarise(Mean=mean(Altura_cm))


sdH=Alturas_Humanos%>%
  dplyr::select(Genero, Altura_cm)%>%
  filter(Genero=="Hombres")%>%
  summarise(sd=sd(Altura_cm))

Aquí el gráfico de la distribución de los datos con un histograma, y promedio (negro), el rango de 68% entre las barras azules y el de 95% entre las barras roja.

Alturas_Mujer=Alturas_Humanos%>%
  dplyr::select(Genero, Altura_cm)%>%
  filter(Genero=="Mujer")%>%
ggplot(aes(Altura_cm))+
  geom_histogram(fill="blue", colour="yellow",alpha=.5)+
  theme(legend.position = "none")+
  geom_vline(xintercept=as.numeric(promM), colour="black")+
  geom_vline(aes(xintercept = as.numeric(promM-sdM)), colour="blue", size=1)+
  geom_vline(aes(xintercept = as.numeric(promM+sdM)), colour="blue")+
geom_vline(aes(xintercept = as.numeric(promM-2*sdM)), colour="red")+
  geom_vline(aes(xintercept = as.numeric(promM+2*sdM)), colour="red")


ggsave("Graficos/Alturas_Mujer.jpeg") # .png, .tiff, etc

Ejercicio: Ahora prepara el mismo gráfico para los hombres.

The tallest building in the world, el numero de pisos

88, 88, 110, 88, 80, 69, 102, 78, 70, 55, 79, 85, 80, 100, 60, 90, 77, 55, 75, 55, 54, 60, 75, 64, 105, 56, 71, 70, 65, 72

Medidas de disperción